[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13]
In your own words, describe how insertion sort works.
We observe that the first element, considered alone, is already in sorted order. We then insert successive elements in the list into this already-sorted segment of the list, each time shifting values back to make room for the element we are inserting. Once the already-sorted segment includes all list elements, we are done.
Complete the following partial implementation of insertion sort so that it reorders its parameter list into increasing order.
def insertion_sort(data):
for i in range(1, len(data)):
t = data[i]
j = i - 1
# Your answer goes here
data[j + 1] = t
def insertion_sort(data):
for i in range(1, len(data)):
t = data[i]
j = i - 1
while j >= 0 and data[j] > t:
data[j + 1] = data[j]
j = j - 1
data[j + 1] = t
In your own words, describe how merge sort works. What is the base case?
The base case is when the array has one element; in this case, nothing happens.
When there is more than one element, merge sort consists of three major steps. First, we split the array into two halves. Then we sort each half through recursively applying the merge sort algorithm to each. And finally, we merge the two halves together by successively “removing” the lesser of the two halves' first elements and placing the removed item into the array holding our result.
Complete the Citizen class below so that
the get_id method returns the id parameter provided
when the Citizen is constructed. The run
function at right illustrates how another function might interact with the
Citizen class.
class Citizen:
def __init__(self, id):
def get_id(self):def run():
b = Citizen(2)
d = Citizen(4)
print(b.get_id()) # displays 2
print(d.get_id()) # displays 4
class Citizen:
def __init__(self, id):
self.ident = id
def get_id(self):
return self.ident
Write a Student class for tracking a
student's grades in CSCI 150.
The class includes two data attributes, both integers: one named
total tracks how many points the student has earned thus
far, and another named possible tracks how many possible
points the student could have earned thus far.
The class includes one constructor and two methods.
Student()(Constructor) Constructs a student who has had completed no graded work for the class.
register(value, poss)Registers that this student has completed work with a grade of
value out of a possible poss.
get_percent()Returns the percent of possible points thus far earned. (The method returns 100.0 when no graded work has been completed.)
The following fragment illustrates how a
program might use the Student class.
robin = Student()
print(robin.get_percent()) # displays 100.0
robin.register(20, 30)
robin.register(10, 20)
print(robin.get_percent()) # displays 60.0
class Student:
def __init__(self):
self.total = 0.0
self.possible = 0.0
def register(self, value, poss):
self.total += value
self.possible += poss
def get_percent(self):
if self.possible == 0.0:
return 100.0
else:
return 100.0 * self.total / self.possible
Complete the Scorecard class below so that the get_sum method returns the total of all the scores given into
the tally method. Thus, a program might use the Scorecard class as follows.
game = ScoreCard()
print(game.get_sum()) # displays 0
game.tally(4)
game.tally(6)
print(game.get_sum()) # displays 10
game.tally(5)
print(game.get_sum()) # displays 15
class Scorecard:
def __init__(self):
def tally(self, score):
def get_sum(self):
class Scorecard:
def __init__(self):
self.total = 0
def tally(self, score):
self.total += score
def get_sum(self):
return self.total
Write a class GolfScore providing the following constructor
and methods.
GolfScore(par)(Constructor) Constructs a score card for tallying scores, where
par is the goal for each score.
add(score)Adds a score onto this score card. (The easiest way to solve this problem is not to remember each individual score added into the card; however, you may approach the problem that way if you wish.)
get_birdie_count()Returns the number of values added into this score card that are
below par.
get_par_difference()Returns the sum over all scores of the difference between the score and the goal. For example, if the goal is 3, and the scores added are 2 and 5, then the method returns 1, since that is the sum of 2 − 3 and 5 − 3.
The following fragment illustrates how a
program might use the GolfScore class.
card = GolfScore(3)
card.add(2)
card.add(3)
card.add(2)
card.add(4)
print(card.get_birdie_count()) # displays 2, since two scores were below 3
print(card.get_par_difference()) # displays -1 (= (2-3) + (3-3) + (2-3) + (4-3))
class GolfScore:
def __init__(self, par):
self.goal = par
self.birdies = 0
self.par_diff = 0
def add(self, score):
if score < self.goal:
self.birdies += 1
self.par_diff += score - goal
def get_birdie_count(self):
return self.birdies
def get_par_difference(self):
return self.par_diff
Write an Interval class for tracking a range of numbers
on the number line. It should have the following constructor and
methods.
Interval(first)(Constructor) Constructs an interval consisting of just
one number, first.
extend(next)If this interval doesn't already contain next, it
is extended just enough to include next.
contains(query)Returns True if this interval contains query.
The below fragment illustrates how this might be used.
Interval i = Interval(5)
print(i.contains(4)) # False
i.extend(2)
i.extend(6)
print(i.contains(4)) # True
print(i.contains(6)) # True
print(i.contains(6.1)) # False
class Interval:
def __init__(self, start):
self.start = start
self.stop = stop
def extend(self, next):
self.start = min(self.start, next)
self.stop = max(self.stop, next)
def contains(self, query):
return self.start <= query <= self.stop
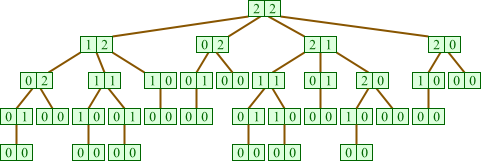
The game of Nim proceeds by players taking turns selecting a pile and removing 1 or more stones from that pile. The player removing the last stone wins.
Draw a complete game tree for the game of Nim beginning with two piles, both containing two stones. To draw a node, list the number of stones in each pile; for example, the top node will be “2,2”.
Do not include the minimax values assigned to each node in your tree.
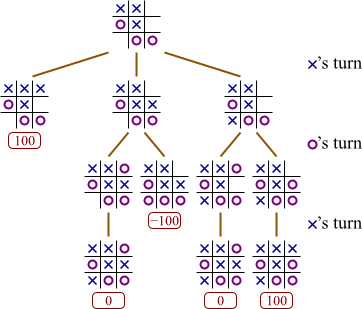
Label all internal nodes of the following tic-tac-toe game tree with the value that minimax search would compute. I've already labeled the leaves.
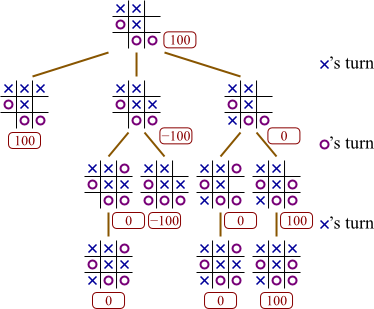
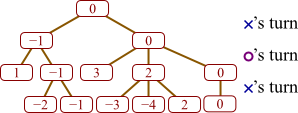
Suppose a game player has constructed a game tree as given below. In this tree, high numbers represent good boards for X, and it is currently X's move.
Fill in all empty circles with the values assigned them according to the minimax evaluation algorithm.
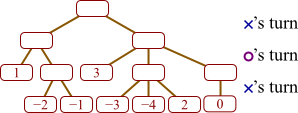
Suppose a game player has constructed the following game tree.
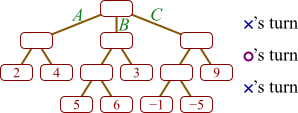
In this tree, high numbers represent good boards for X, and it is currently X's move. (As you can see, X has three possible moves from which to choose, labeled A, B, and C.)
| a. | 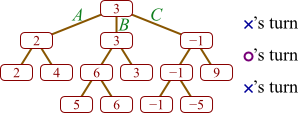 |
b. | B |
Suppose we have developed the below game tree through recursive evaluation, in an attempt to find the value of node A. According to alpha-beta search, node C need not be evaluated. Explain why. (In this example, we are imagining that at A, it is X's turn, and larger numbers denote a more positive situation for X.)
Let's start by considering B. At B it is O's turn, and O will choose the smaller of 0 and C's value. Thus, the value of B will be 0 or less. At A it is X's turn, and X choose the larger of 3 and whatever B's value will turn out to be. But since we know B will be 0 or less, so it will inevitably choose 3, regardless of whatever C might turn out to be. So if we simply want to know A's value, we need not bother with determining C's value.