Review 6: Dynamic programming: Questions
Consider the following recursive algorithm.
public static int f(int n, int r) {
if(r == 0 || r >= n) return 1;
else return f(n - 1, r - 1) + f(n - 1, r);
}
Using dynamic programming, convert this into a method that takes O(n ⋅ r) time.
Suppose we are playing a series of games against an opponent for which we have a probability p of winning, and we want to know the probability that we'll win k of the next n games against our opponent. Below is a recurrence for computing this.
| P(k, n) = { | 0 | if k > n |
| (1 − p)n | if k = 0 | |
| p ⋅ P(k − 1, n − 1) + (1 − p) ⋅ P(k, n − 1) | if k > 0 and k ≤ n |
Use dynamic programming to complete the below Java method to compute this value in O(n ⋅ k) time.
public static double computeProbabilityKofN(int k, int n, double p) {
Software for typesetting text must automatically decide where to place the line breaks between words in a paragraph. One approach for this, used in high-quality typesetting programs such as TEX, is to define a cost function computing with the “badness” of each line, defined by a function c(i, j), which might be defined as ∞ if the line including words i through j simply is too long to fit into the available space; but if the words fit, it yields a number such as
(You don't have to worry about this formula for this problem.)
Assuming we have the “badness” function already defined, we can write a recurrence for computing the smallest overall badness for each possible way to break lines in a paragraph of words.
| f(j) = { | c(1, j) | if c(1, j) ≠ ∞ |
| min1 ≤ k < j (f(k) + c (k + 1, j)) | if c(1, j) = ∞ |
Using dynamic programming, convert this recurrence into a Java
method that takes O(n²) time, assuming
that a method c has already been defined and takes
O(1) time for each invocation. The c method
returns Integer.MAX_VALUE to signify an infinite return
value.
public static int f(int n) {
You run a factory that manufactures only one item, which can be either a widget or a gizmo. Your team of analysts have predicted the demand for widgets and gizmos for each of the upcoming T weeks and determined that you will earn a profit of p0, t dollars in week t (where 1 ≤ t ≤ T) if you choose to make widgets that week and p1, t dollars if you choose to make gizmos. All profits are nonnegative.
However, switching your factory from widgets to gizmos isn't cheap: You have to fire all your old widget-makers and hire a new team of gizmo-makers, and you have to switch out all your equipment. Overall, the switching process takes two weeks during which no product is produced, and it costs s dollars, whether switching from widgets to gizmos or vice versa.
Using dynamic programming, describe an O(T) algorithm that determines the maximum profit. Feel free to express the main part of your algorithm as a recurrence.
A roadside advertising company hires you to find an algorithm for selecting billboard sites. They have rights to n locations along a road, each identified by its mile marker mi. They know the revenue ri that will be earned from each potential location. However, they are not allowed to erect billboards within 10 miles of each other.
Construct an algorithm that determines the maximum revenue that can be obtained by building at most k billboards.
In the knapsack problem, we imagine we're given some capacity c and a list of n weights w0, w1, … wn − 1. The following recurrence solves it, leading to a dynamic programming solution that takes O(c ⋅ n) time.
| K(c, n) = { | 0 | if n = 0 |
| K(c, n − 1) | if wn − 1 > c | |
| max { K(c, n − 1), wn − 1 + K(c − wn − 1, n − 1) } | otherwise |
Suppose our knapsack also has a limit that restricts it from holding more than k items? How can we modify our recurrence to lead to a dynamic programming solution that takes O(c ⋅ n ⋅ k) time?
Recall that we could find a dynamic programming solution to the edit distance problem using the following recurrence.
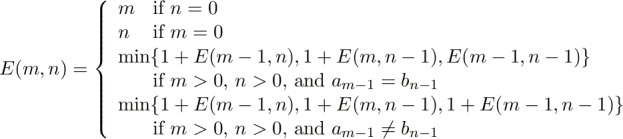
Suppose we decide that adding an extra apostrophe is not a serious error, and so we want to count it as just a half-point in the distance formula. Thus, the distance from wits to it's is 1.5 steps rather than 2 as by the above recurrence. How could we modify the recurrence to address this?
Review 6: Dynamic programming: Solutions
public static int f(int n, int r) {
int[][] sub = new int[n + 1][r + 1];
for(int ni = 0; ni <= n; ni++) {
for(int ri = 0; ri <= r; ri++) {
if(ri == 0 || ri >= ni) sub[ni][ri] = 1;
else sub[ni][ri] = sub[ni - 1][ri - 1] + sub[ni - 1][ri];
}
}
return sub[n][r];
}
public static double computeProbabilityKofN(int k, int n, double p) {
double[][] prob[k + 1][n + 1];
for(int ni = 0; ni <= n; ni++) {
for(int ki = 0; ki <= k; ki++) {
if(ki > ni) {
prob[ki][ni] = 0;
} else if(ki == 0) {
prob[ki][ni] = Math.pow(1 - p, ni)
} else {
prob[ki][ni] = p * prob[ki - 1][ni - 1]
+ (1 - p) * prob[ki][ni - 1];
}
}
}
return prob[k][n];
}
public static int f(int n) {
int[] table = new int[n + 1];
for(int j = 1; j <= n; j++) {
if(c(1, j) == Integer.MAX_VALUE) {
int min = Integer.MAX_VALUE;
for(int k = 1; k < j; k++) {
int cv = c(k + 1, j);
if(cv != Integer.MAX_VALUE) {
if(table[k] + cv < min) min = table[k] + cv;
}
}
table[j] = min;
} else {
table[j] = c(1, j);
}
}
return table[n];
}
We define the recurrence P(i, t), which represents the most profit that can be made in the first t weeks if we need to be ready to produce product i in week t + 1.
| P(i, t) = { | 0 | if t = 0 |
| pi, 1 | if t = 1 | |
| max { pi, t + P(i, t − 1), −s + P(1 − i, t − 2) } | if t > 1 |
With this recurrence defined, we use dynamic programming to compute both P(0, T) and P(1, T). The larger of these two values is the maximum profit obtainable within T weeks.
Define R(i, j) as the best revenue that can be earned by erecting a billboard at location i and j − 1 billboards at location previous to i. This can be computed using the below recurrence.
| R(i, k) = { | 0 | if k = 0 |
| r_i | if k > 0 and i = 0 | |
| r_i + maxj : mj ≤ m{i − 10} R(j, k − 1) | if k > 0 and i > 0 |
Once we have this, we return the largest value of R(i, k) over all i.
| K(c, n, k) = { | 0 | if n = 0 or k = 0 |
| K(c, n − 1, k) | if wn − 1 > c | |
| max { K(c, n − 1, k), wn − 1 + K(c − wn − 1, n − 1, k − 1) } | otherwise |