Test 3 Review A
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21]
Problem R3a.1.
Programs normally store sorted data in a red-black tree (as with Java's TreeSet class) or some other form of balanced binary tree. Why is this approach unsuitable for database management systems to store their indexes (which leads to their using B+-trees instead)?
A node in a red-black tree has relatively little data, taking up far less than a block of disk storage. As a result, a lookup in the index will require reading many disk blocks to reach a leaf; by contrast, a B+-tree, which has a higher branching factor with each block, requires many fewer disk blocks to reach a leaf.
Problem R3a.2.
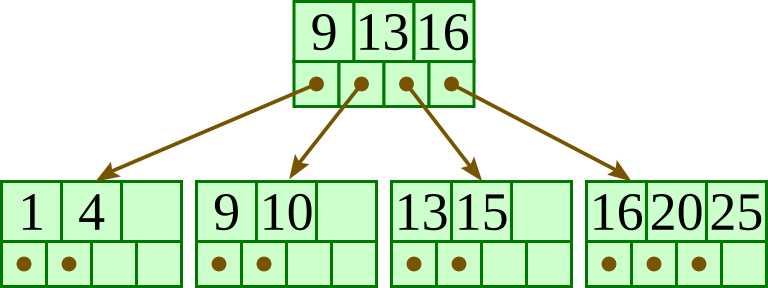
For the below B+-tree, each node contains up to three keys and four pointers. Show the B+-tree that would result by inserting 4 as described in class.

Problem R3a.3.
For the below B+-tree, each node contains up to three keys and four pointers. Show the B+-tree that would result by inserting 5 as described in class.


Problem R3a.4.
For the below B+-tree, each node contains up to three keys and four pointers. Show the B+-tree that would result by inserting 5 as described in class.


Problem R3a.5.
For the below B+-tree, each node contains up to three keys and four pointers. Show the B+-tree that would result by inserting 4 as described in class.


Problem R3a.6.
For the below B+-tree, each node has up to three keys and four pointers. Show the B+-tree that would result by inserting 10 as described in class.

Problem R3a.7.
For the below B+-tree, each node contains up to three keys and four pointers. Show the B+-tree that would result by deleting 11 as described in class.

Problem R3a.8.
Suppose that each node of a B+-tree has up to five keys and six pointers. If this tree has 100 keys represented among its leaves, what is the maximum number of levels it might have (that is, the maximum number of disk accesses to find any individual key among its leaves)? Explain your answer.
Overall, the tree will have at most four levels. To get the deepest tree possible, we will need to maximize the number of nodes at each level.
Let us start from the bottom level — the leaves. Each leaf must have at least three keys, so the largest number of leaves possible is 100/ 3 = 33. (It does not divide exactly, but 33 is the largest possible; 34 leaves would require at least 34 ⋅ 3 > 100 keys.)
At the level above the leaves, each node must point to at least three leaves as children, so the largest number of nodes in this levels is 33 / 3 = 11.
The level above these will have at most 11 / 3 = 3 nodes.
The level above these will have only one node, the root.
Problem R3a.9.
Suppose we have a B+-tree indexing a table of 1,000,000 records, where each node can hold a maximum of 19 keys and 20 pointers. How many disk accesses (at most) would be required to load a record with a given key value into memory? Justify your answer.
There would be at most 8 block reads with each access. The root node will have at least two pointers, so reading it and traversing a pointer will go into a half of the tree with at most 500,000 records. The next node will have at least 10 pointers, so traversing a pointer will go into a subtree with at most one-tenth of the records, or 50,000. Likewise, reading the third node will reduce the number of records to 5,000; the fourth to 500; the fifth to 50; the sixth to 5; and the seventh read, which will be of a leaf, will give us the location of the block within the table. Once we get the location within the table, we then must look into the actual table to retrieve the record, and that will require an eighth disk read.
Problem R3a.10.
The following pseudocode describes an algorithm that requires B(R) + (T(R) B(S)) disk accesses. Explain how it can be changed to require only B(R) + (B(R) B(S) / (M − 1)) accesses.
for each tuple r in R:
for each block U in S:
for each tuple s in U:
if r and s have the same join key:
output r, s
We use the other blocks of memory so we read many blocks from R, and join all those tuples with each tuple from S. We consequently end up going through S many fewer times — in fact, we go through it B(R) / (M − 1) times. Each time requires B(S) block reads, so the total number of accesses is B(R) + (B(R) B(S) / (M − 1)).
while more blocks remain in R:
read next M − 1 blocks from R
for each block U in S:
for each tuple r in the M − 1 blocks:
for each tuple s in U:
if r and s have the same join key:
output r, s
Problem R3a.11.
We saw in class that a nested-loop join of two relations R and S takes B(R) + (B(R) B(S) / (M − 1)) disk accesses. But we also saw algorithms that take c (B(R) + B(S)) disk accesses for some constant c like 3 or 5. Select one such algorithm to describe; describe it, and explain why we approximate the number of disk accesses by c (B(R) + B(S)).
[We saw a few ways in class. I'll describe the simplest.] Do a two-phase multiway merge-sort of R based on the join key; this will require two passes through R. Similarly, do a two-phase multiway merge-sort of S based on the join key. Then go through one more pass of the two sorted relations in parallel, as if we were merging them; whenever we find two rows sharing the same join key values, we output a row containing the attributes of those two rows.
Problem R3a.12.
Suppose our DBMS's algorithm for joining R and S to get R × S takes B(R) + B(R) B(S) disk accesses. Suppose, moreover, that we wish to compute A × B × C, where the number of disk blocks in each relation (and possible joins of relations) is as follows:
| A | 100 | A × B | 100 | B × C | 40 | ||
| B | 40 | A × C | 1,000 | A × B × C | 100 | ||
| C | 10 |
How many disk accesses will it take for each of the following?
a. Compute A × B, then join the result with C.
b. Compute A × C, then join the result with B.
c. Compute B × C, then join the result with A.
a. Joining A and B will take 100 + 100 ⋅ 40 = 4,100 accesses, and joining this with C will take 100 + 100 ⋅ 10 = 1,100 accesses, for a total of 4,100 + 1,100 = 5,200.
b. Joining A and C will take 100 + 100 ⋅ 10 = 1,100 accesses, and joining this with B will take 1,000 + 1,000 ⋅ 40 = 41,000 accesses, for a total of 1,100 + 41,000 = 42,100.
c. Joining B and C will take 40 + 40 ⋅ 10 = 440 accesses, and joining this with A will take 40 + 40 ⋅ 100 = 4,040 accesses, for a total of 440 + 4,040 = 4,480.
Problem R3a.13.
Suppose we want to sort a very large file of fixed-length records. Let L be the number of blocks in the file, and let M be the number of blocks available in memory. Describe an algorithm that can sort the file using at most 4L disk accesses, assuming that M < L ≤ M² − M.
runsof M blocks each, and we do an in-memory sort on each run, storing the sorted run onto disk. This will require 2 L accesses: We'll access each block of the file to load it into memory, and then we'll store the sorted runs onto the disk. There will be at most M − 1 runs.
In the second phase, we merge all the runs by loading the first block of each run into memory and merging them together into an additional block. As we merge together and fill this destination block, we'll write that into the overall sorted output; and as we deplete the first block from each run, we replace that block of memory with the following block in the run. This second phase will again load each block of each run, requiring another L loads; and it will store the sorted file, taking another L stores.
Problem R3a.14.
Let M be the number of blocks available in memory. To use two-phase multiway merge sort on a file, what is the maximum size of the file? Explain your answer.
The file can have at most M² − M blocks, so that it can be broken up into M − 1 chunks of M blocks each. In the first phase, we sort each chunk independently. In the second phase, we will need to load the a block of each chunk into memory as we merge the M − 1 chunks together (saving the remaining block for accumulating the sorted output).
Problem R3a.15.
Describe the concept of a transaction in database management systems.
A transaction is a group of related database operations that should be completed as a group. That is, if any of the operaions in the transaction modify the databases, then all of the operations in the transaction must be completed.
Problem R3a.16.
Identify and explain what the A stands for among the ACID database properties.
Atomicity is the property that the operations requested by a transaction will either all be completed or all have no effect.
Problem R3a.17.
Identify and explain what the I stands for among the ACID database properties.
Isolation means that transactions should be completed as if they were in isolation, behaving as if one transaction starts and finishes before another is allowed to start.
Problem R3a.18.
Identify and explain what the D stands for among the ACID database properties.
Durability means for each committed transaction, its results will persist no matter what happens in the future. Even if the computer crashes, the transaction's results should still endure. (This is typically accomplished by writing enough information onto disk before the transaction completes.)
Problem R3a.19.
Suppose we have two transactions:
ID action operations 1. Decrease A by 100. r1(A), w1(A) 2. Increase A by 100. r2(A), w2(A)
Suppose A starts at 500. Write three different valid schedules for these transactions, each resulting in a different final value for A, and identify the final value for A for that schedule.
- r_1(A), w_1(A), r_2(A), w_2(A) (or r_2(A), w_2(A), r_1(A), w_1(A))
- A ends up at 500.
- r_1(A), r_2(A), w_1(A), w_2(A) (or r_2(A), r_1(A), w_1(A), w_2(A))
- A ends up at 600.
- r_1(A), r_2(A), w_2(A), w_1(A) (or r_2(A), r_1(A), w_2(A), w_1(A))
- A ends up at 400.
Problem R3a.20.
Draw a precedence graph for determining whether the schedule below is conflict-serializable, labeling each edge with the operations that lead you to include that edge.
w1(A), w2(B), w3(C), w1(B), w2(C), w3(A)
With specific reference to your graph, explain whether you can conclude that the schedule is conflict-serializable.
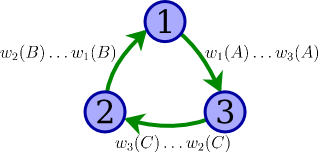
Because the precedence graph contains a cycle (1 → 3 → 2 → 1), we can conclude that the schedule must not be conflict-serializable.
Problem R3a.21.
Draw a precedence graph for determining whether the schedule below is conflict-serializable.
w1(A), r2(A), w2(B), r3(A), w4(B), w4(C), r3(C), r1(C)
With specific reference to your graph, explain whether you can conclude that the schedule is conflict-serializable.
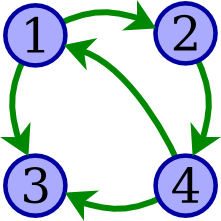
This graph indicates that the schedule is not conflict-serializable, due to the cycle 1 → 2 → 4 → 1. (There are no other cycles in this graph.)


