Next: Mergesort. Up: Recursion. Previous: Fibonacci numbers.

Towers of Hanoi

The Towers of Hanoi puzzle involves a set of discs of different sizes, stacked on one of three pegs.

The goal is to move the discs from the left peg to the center peg, moving only one disc at a time between pegs, and never placing a larger disc atop a smaller disc.

We can write down a recipe for solving the puzzle as follows.

  1. Move the subtower above the largest disc in the tower to the spare peg using this recipe.

  2. Move the largest disc in the tower to the destination peg.

  3. Move the subtower above the largest disc in the tower to the destination peg using this recipe.

Or perhaps it's easier if I just write down the Java code for printing out the solution. In this solution, I've numbered the discs beginning with 0 for the smallest disc, and I've lettered the pegs 'A', 'B', and 'C'. 
import csbsju.cs160.*;

public class Hanoi {
    public static void main(String[] args) {
        printSolution(2, 'A', 'B');
    }
    private static void printSolution(int disc, char from, char dest) {
        if(disc == 0) {
            System.out.println("Move " + disc + " from " + from
                + " to " + dest);
        } else {
            char spare;
            if(from != 'A' && dest != 'A')      spare = 'A';
            else if(from != 'B' && dest != 'B') spare = 'B';
            else                                spare = 'C';

            printSolution(disc - 1, from, spare);
            System.out.println("Move " + disc + " from " + from
                + " to " + dest);
            printSolution(disc - 1, spare, dest);
        }
    }
}

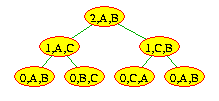
Here's the recursion tree for moving three discs.

This program illustrates something about recursion that we haven't seen before, but it's not immediately obvious: Notice the local spare variable. Its value changes three times in the above recursion tree: Once at the (2,A,B) node (when its value becomes 'C'), once at the (1,A,C) node (when its value becomes 'B'), and once at the (1,C,B) node (when its value becomes 'A'). Between the second and third times, the (2,A,B) node calls printSolution(disc-1,spare,dest).

You might think that at this time, spare's value is 'B', since the last time spare was altered (in the (1,A,C) node), this was the new value. But that's not what happens. Every recursive call gets its own set of local variables. Thus, the change in value to spare in the (1,A,C) node only affects the spare variable allocated for that node. The spare variable in the (2,A,B) node remains unchanged at 'C'. The recursive calls to printSolution from the (2,A,B) node use this variable, so that the second recursive call actually still moves from 'C' to 'B'.

Next: Mergesort. Up: Recursion. Previous: Fibonacci numbers.