Fibonacci numbers
Towers of Hanoi
Mergesort
Mergesort algorithm
Java code
Theoretical time analysis
Experimental speed analysis
Recursion is the concept of something being defined in terms of itself. It sounds like it's circular - but it's not necessarily so. A circular definition, like defining a rose as a rose, is termed infinite recursion. But some recursive definitions aren't circular: They have a base case, where the recursive definition no longer applies, and the definition for any other case eventually reaches the base case.
In mathematics, things are often defined recursively. For example, the Fibonacci numbers are often defined recursively. The Fibonacci numbers are defined as the sequence beginning with two 1's, and where each succeeding number in the sequence is the sum of the two preceeding numbers.
We obtained 8 in the above sequence by summing the previous two numbers (3 and 5).1 1 2 3 5 8 13 21 34 55 ...
A formal mathematical definition would define this using mathematical symbols.
1 if n = 0 or n = 1
F(n) = {
F(n-1) + F(n-2) otherwise
In computer programming, also, it's often convenient to define something recursively. And Java allows you to do this - all you have to do is to use the function within its own definition. The following program computes and prints a Fibonacci number requested by the user.
import csbsju.cs160.*;
public class Fibonacci {
public static void main(String[] args) {
IO.println("Which Fibonacci? ");
IO.println("It is " + fib(IO.readInt()));
}
private static int fib(int n) {
if(n <= 1) return 1;
else return fib(n - 1) + fib(n - 2);
}
}
Notice how the recursive function has its base case - in this example, the base case is when n is at most 1, when the program returns 1 without any further recursive calls. Recursive programs must always have a base case! Novices tend to forget to include a base case when programming.
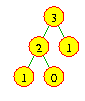
As a programmer, it's important that you understand how this works within the computer. The computer will go through the following process to compute fib(3):
3 exceeds 1, so I need to compute and return fib(3 - 1) + fib(3 - 2).
To compute this, I first need to compute fib(2).
2 exceeds 1, so I need to compute and return fib(2 - 1) + fib(2 - 2).
To compute this, I first need to compute fib(1).
1 is less than or equal to 1, so I need to return 1.
Now that I know fib(1), I need to compute fib(0).
0 is less than or equal to 1, so I need to return 1.
I now know fib(2 - 1) + fib(2 - 2) = 1 + 1 = 2. I return this.
Now that I know fib(2) is 2, I need to compute fib(1).
1 is less than or equal to 1, so I need to return 1.
I now know fib(3 - 1) + fib(3 - 2) = 2 + 1 = 3. I return this.
It helps to draw a recursion tree to illustrate the different recursive calls entered in the process of the computation. A recursion tree has a node for each call of the method, connected by a line to the method call that called it. For the example of fib(3), the recursion tree would be as follows.

The Towers of Hanoi puzzle involves a set of discs of different sizes, stacked on one of three pegs.
We can write down a recipe for solving the puzzle as follows.
import csbsju.cs160.*;
public class Hanoi {
public static void main(String[] args) {
printSolution(2, 'A', 'B');
}
private static void printSolution(int disc, char from, char dest) {
if(disc == 0) {
System.out.println("Move " + disc + " from " + from
+ " to " + dest);
} else {
char spare;
if(from != 'A' && dest != 'A') spare = 'A';
else if(from != 'B' && dest != 'B') spare = 'B';
else spare = 'C';
printSolution(disc - 1, from, spare);
System.out.println("Move " + disc + " from " + from
+ " to " + dest);
printSolution(disc - 1, spare, dest);
}
}
}
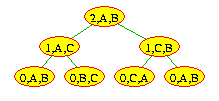
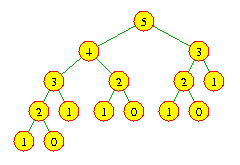
This program illustrates something about recursion that we haven't seen before, but it's not immediately obvious: Notice the local spare variable. Its value changes three times in the above recursion tree: Once at the (2,A,B) node (when its value becomes 'C'), once at the (1,A,C) node (when its value becomes 'B'), and once at the (1,C,B) node (when its value becomes 'A'). Between the second and third times, the (2,A,B) node calls printSolution(disc-1,spare,dest).
You might think that at this time, spare's value is 'B', since the last time spare was altered (in the (1,A,C) node), this was the new value. But that's not what happens. Every recursive call gets its own set of local variables. Thus, the change in value to spare in the (1,A,C) node only affects the spare variable allocated for that node. The spare variable in the (2,A,B) node remains unchanged at 'C'. The recursive calls to printSolution from the (2,A,B) node use this variable, so that the second recursive call actually still moves from 'C' to 'B'.
The final sorting algorithm we'll examine in the class works using an algorithmic design technique called divide and conquer. In this case, we first split the array into two halves, then we sort each half (using the same procedure - i.e., we make a recursive call), and finally we merge the two halves together. The base case would be when the array has only one element in it, in which case it is already sorted. This algorithm is called Mergesort.
Writing Mergesort in Java is significantly more complex that writing selection sort or insertion sort: The basic procedure (the sort() method) isn't bad. But merging two arrays into one is a relatively complex to write itself. (It's implemented below in the merge() method. Basically, it starts at the front of both arrays to be merged; the minimum of these goes at the front of the merged array. And then it can step to the next element of the array to repeat the process to see which is second, which is third, etc.) This implementation also defines a method extract() for extracting a subarray of a larger, known array.
public class MergeSort {
// sort: reorders the elements of elts so that they are in
// increasing order.
public static void sort(int[] elts) {
if(elts.length > 1) {
// split the array into two pieces, as close to the same
// size as possible.
int[] first = extract(elts, 0, elts.length / 2);
int[] last = extract(elts, elts.length / 2, elts.length);
// sort each of the two halves recursively
sort(first);
sort(last);
// merge the two sorted halves together
merge(elts, first, last);
}
}
// extract: returns a subarray of elts, starting with index
// start in elts, continuing to (but not including) index
// last.
private static int[] extract(int[] elts, int start, int last) {
int[] ret = new int[last - start];
for(int i = 0; i < ret.length; i++) ret[i] = elts[start + i];
return ret;
}
// merge: merges arrays a and b, placing the result into the
// array dest. This only works if both a and b are already in
// increasing order.
private static void merge(int[] dest, int[] a, int[] b) {
int i = 0;
int j = 0;
while(i < a.length && j < b.length) {
if(a[i] < b[j]) {
dest[i + j] = a[i];
++i;
} else {
dest[i + j] = b[j];
++j;
}
}
for(; i < a.length; i++) dest[i + j] = a[i];
for(; j < b.length; j++) dest[i + j] = b[j];
}
}
(From a programming point of view, this particular implementation is pretty inefficient: It allocates quite a bit more memory than necessary, which wastes a lot of time. I've sacrificed efficiency for readability here, which is fine, since optimizing to this level of detail isn't really a part of this course. But I just wanted to include this little footnote to point out that all this memory allocation isn't the best way of going about this program.)
To get a feel for how this works, we first analyze the process of extracting two subarrays and merging the two subarrays. If the original array has n elements, then both of these take O(n) time. (In the extract() method, this is easy to see. In the merge() method, you can convince yourself of this by observing that, each time through any of the loops, the sum i + j increases by 1. This sum begins at 0, and it never exceeds n, so the total number of times through all the loops must be at most n (and in fact it's exactly n).)
With this observation, we could define a recurrence T(n) representing how much time it takes to Mergesort an array of length n.
O(1) if n <= 1
T(n) <= {
O(n) + 2 T(n / 2) + O(n) otherwise
Unfortunately, we haven't the mathematical machinery to do this right now. But there's an easier way. Let's assume that n is a power of 2, to simplify our analysis. Then let's draw a recursion tree.
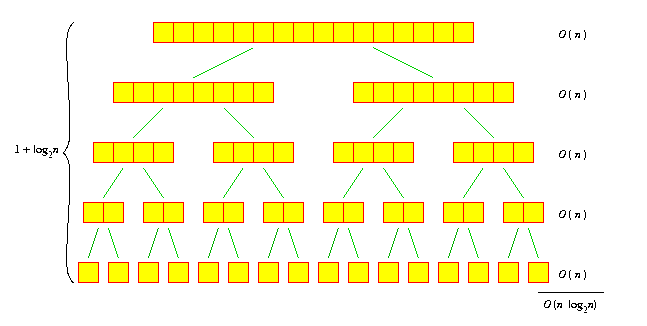
Say we're at a node handling an array of length k. For this node, the time spent outside the recursive calls is O(k) - after all, it takes O(k) time to split the array into two and O(k) time to merge the two sorted arrays together. (And for the base cases at the bottom, for all of which k=1, it takes O(1) time to simply return having changed nothing.)
We'll sum up the times for each node, by summing by horizontal levels. For each level, the sum of the times for each node is O(n). Since the size of the arrays in each level halves each time we go down, we can immediately see that there are 1 + log2 n levels. So the total amount of time is O(n log2 n).
This is dramatically better than O(n2). But that's a theoretical result, and you might justifiably wonder how it compares in practice.
To see how Mergesort performs in practice, I used the code from today and last time, and wrote a short program to time the various algorithms on different sizes of arrays. Here are the numbers I collected. (Times are in milliseconds, measured on a SunBlade 100, which has a 500MHz SPARC chip in it.)
| n | selection | insertion | merge |
|---|---|---|---|
| 100 | 0.233 | 0.093 | 0.160 |
| 200 | 0.874 | 0.377 | 0.345 |
| 300 | 1.955 | 0.927 | 0.541 |
| 400 | 3.519 | 1.553 | 0.743 |
| 500 | 5.417 | 2.507 | 0.958 |
| 600 | 7.746 | 3.672 | 1.161 |
| 700 | 10.630 | 5.088 | 1.373 |
| 800 | 13.929 | 6.342 | 1.589 |
| 900 | 17.590 | 8.146 | 1.821 |
| 1000 | 21.799 | 9.622 | 2.059 |
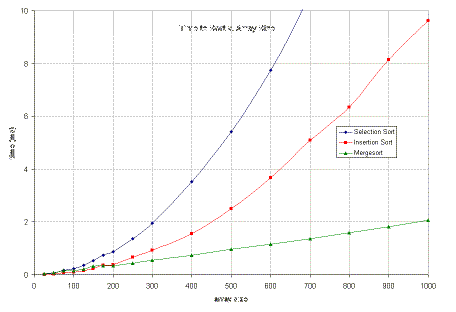
You can see that for small arrays (less than 200 elements), all three techniques do well (and in fact sometimes Mergesort does worse than the other two). But, as the arrays get to be moderately large, it quickly does quite a bit better.
Plus, the Mergesort I timed wasn't very optimized. If I really wanted to write decent Mergesort code, I could easily cut its computation time to a fraction of the measured time. (In fact, I wrote an optimized version, which takes a third of the time of the MergeSort presented above (pretty much regardless of array size).) The same isn't true of insertion sort or selection sort, both of which are very close to the best possible implementation.
(As a footnote, I also tried to do some timings with C++, just to see how it would perform relative to the Java code. Since the Java code is running under the JVM, it has an inherent disadvantage, and I expected to see the C++ program doing much better. Surprisingly, the straightforward C++ translation of the above Mergesort code seemed to do about 50% worse than the Java code. The C++ translation of the optimized Java version, however, ran three times as fast as its Java equivalent - that is, 9 times as fast as the straightforward Java code above: on a random length-1000 array, it took only 0.101 milliseconds to sort.)