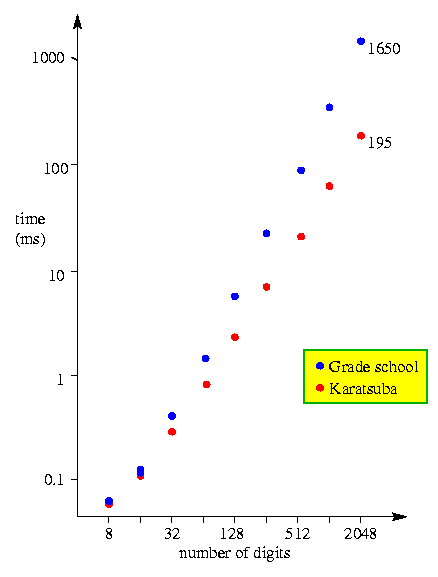
Graph of results (Note the logarithmic axes)
Next: None. Up: Multiplying. Previous: Divide-and-conquer multiplication.

In January 1999, I implemented the program in C++ and timed it on a Sun SPARCstation 4. (It was an antiquated computer even at that time. A later test on a 700MHz Pentium II did about 50 times better.) The below results are the results for pairs of random n-digit numbers. (Yes, digits. I implemented it in decimal.) All times are in milliseconds.
| # digits | divide-and-conquer | grade school |
|---|---|---|
| 8 | 0.059923 | 0.063902 |
| 16 | 0.106360 | 0.121773 |
| 32 | 0.278862 | 0.414594 |
| 64 | 0.798085 | 1.481481 |
| 128 | 2.325581 | 5.780347 |
| 256 | 6.944444 | 22.727273 |
| 512 | 21.276596 | 88.333333 |
| 1024 | 63.750000 | 370.000000 |
| 2048 | 195.000000 | 1650.000000 |
Of course, this begs the question: Why would one want to multiply 100-digit numbers with exact precision? One response is cryptographic applications: Some protocols (including RSA) involve many multiplications of keys with hundreds of digits. (Another application is to breaking mathematical records (largest prime, whatever), but it's not clear how practical this is.)
Next: None. Up: Multiplying. Previous: Divide-and-conquer multiplication.