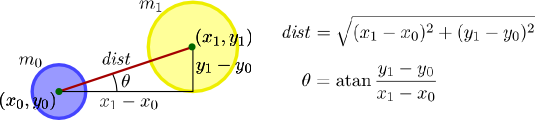

In this assignment we'll simulate the law of gravity to illustrate the motions of the sun and the planets of inner solar system: Mercury (cyan), Venus (green), Earth (blue), and Mars (red), as well as a comet based on Comet Encke (magenta), which has an orbit of 3.3 earth years.
I have already started the program, as linked below; your job
is to complete its Body class, which will incorporate
the code computing how gravity affects each body of the system.
| ACM API | Swing API | |
| SolarSystem.java | SolarSystem.java | |
| Body.java | Body.java |
The Body class should incorporate the following constructor and
methods. (You'll notice I've also included a toString method,
but it's just in case you want it for debugging. You don't need to use
it.)
Body(double inMass, String inName, double inVx, double inVy)(Constructor) Constructs a body with the given mass and name.
Its initial velocity in the horizontal direction is inVx pixels
per frame,
and its initial velocity in the vertical direction is
inVy pixels per frame.
double getMass()Returns the mass of this body.
void updateDirection(SolarSystem system)Updates the velocity of this body based on the bodies within
win. The physics of how the body is affected are described
below.
Note that this method does not alter the velocity of other bodies in the
window. The window will invoke updateDirection for every body,
and each invocation will update the velocity only for that body.
void step()Moves the body one step according to its current direction.
Suggestion: I recommend starting by writing all
the methods but updateDirection, and just leaving
updateDirection blank. Thus, you wouldn't need to worry
at first about the mathematics listed below. There would be no gravity, and
so all the bodies would move in straight lines. Only after you see this
much working would you start on updateDirection.
Gravity exerts a force between each pair of bodies. Suppose we have two bodies, one of mass m0 at (x0, y0), and another of mass m1 at (x1, y1). We can determine the distance and angle between them as diagrammed below.
I recommend using the Math class's
atan2 method to compute θ. It takes two
parameters, the first being the numerator of the above fraction,
y1 − y0,
and the second being the denominator,
x1 − x0.
It returns the angle in radians.
Of course, m0 will have some current velocity, moving vx pixels in the x-direction with each time frame and vy pixels in the y-direction. But gravity will lead this mass m0 to be pulled toward m1; the law of gravity says that it will be pulled with a force of:
The gravitational constant G used in the above formula is 6.67 × 10−30. (The actual gravitational constant is 6.67 × 10−11 m³ / kg s²; but in our program each pixel represents 109 meters, and each frame represents 104 seconds; after converting the units to pixels and frames, we arrive at the exponent of −30.)
The force thus computed will lead vx to increase by F cos θ and vy to increase by F sin θ.
Of course, there are several bodies in the solar system. The same body m0 will be pulled by all other bodies; thus, to update the velocity of a body, you would go through all other bodies, compute the force pulling it toward that body, and update its velocity accordingly.