Section 2.1:
[1]
[2]
[3]
[4]
[5]
[6]
Section 2.2:
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
Define the term base case as it applies to recursive methods, and explain why every recursive method that works correctly must have at least one.
A base case is a condition under which a method that is normally recursive makes no recursive calls. Every recursive method must have such a case — otherwise, a call to the method will result in another call, which results in another call, ad infinitum, and the recursive method will never get to a point when it can return.
Consider the following recursive class method.
public static int f(int n) {
if(n <= 1) {
return 1;
} else {
return f(n - 1) + f(n / 2);
}
}
Draw the recursion tree illustrating how this function would compute
f(5).

A text description:
5 is at the root, with children 4 and 2.
The root's child 4 has children 3 and 2.
The root's child 2 has children 1 and 1, both of which have no children.
The root's grandchild 3 (whose parent is 4) has children 2 and 1.
The root's grandchild 2 (whose parent is also 4) has children 1 and 1.
The root's great-grandchild 2 (whose parent is 3) has children 1 and 1, both of which have no children.
The root's great-grandchild 1 (whose parent is 3) has no children.
Draw a recursion tree
representing the recursive calls made to f in the course of
computing the value of f(11) using the following
method.
public static void f(int n) {
if(n <= 1) {
return 1;
} else if(n % 2 == 0) {
return 2 * f(n / 2);
} else {
return f((n - 1) / 2) + f((n + 1) / 2);
}
}
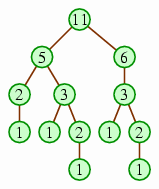
A text description:
11 is at the root, with children 5 and 6.
The root's child 5 has two children, labeled 2 and 3.
The root's child 6 has one child, labeled 3.
The root's grandchild 2 (whose parent is 5) has one child, labeled 1.
The root's grandchild 3 (whose parent is also 5) has two children, labeled 1 and 2.
The root's grandchild 3 (whose parent is 6) has two children, labeled 1 and 2.
The root's great-grandchild 2 (whose parent is 3, which is below 5) has one child, labeled 1.
The root's other great-grandchild 2 (whose parent is 3, which is below 6) has one child, labeled 1.
All of the nodes labeled 1, which include three great-grandchildren and two great-great-grandchildren, have no children.
Suppose we define f as below. Draw a recursion tree
diagramming the computation of f(4, 2).
public static int f(int n, int r) {
if(r == 0 || r == n) return 1;
else return f(n - 1, r) + f(n - 1, r - 1);
}

A text description:
At the root is a node labeled (4,2), with children (3,2) and (3,1).
The root's child (3,2) has two children, labeled (2,2) and (2,1).
The root's child (3,1) has two children, labeled (2,1) and (3,0).
The root's grandchild (2,2) (whose parent is (3,2)) has no children.
The root's grandchild (2,1) (whose parent is also (3,2)) has two children, labeled (1,1) and (1,0).
The root's grandchild (2,1) (whose parent is (3,1)) has two children, labeled (1,1) and (1,0).
The root's grandchild (3,0) (whose parent is also (3,1) has no children.
All of the great-grandchildren have no children.
Suppose we define f as below. Draw a recursion tree
diagramming the computation of f(3, 2).
static int f(int m, int n) {
if(m == 0 || n == 0) return 0;
else return f(m, n - 1) + f(m - 1, n);
}
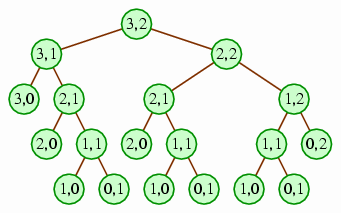
A text description:
At the root is a node labeled (3,2), with children (3,1) and (2,2).
The root's child (3,1) has two children, labeled (3,0) and (2,1).
The root's child (2,2) has two children, labeled (2,1) and (1,2).
The root's grandchild (3,0) (whose parent is (3,1)) has no children.
The root's grandchild (2,1) (whose parent is also (3,1)) has two children, labeled (2,0) and (1,1).
The root's grandchild (2,1) (whose parent is (2,2)) has two children, labeled (2,0) and (1,1).
The root's grandchild (1,2) (whose parent is also (2,2) has two children, labeled (1,1) and (0,2).
All of the great-grandchildren labeled (2,0) and (0,2) have no children. The three great-grandchildren labeled (1,1) have two children each, labeled (1,0) and (0,1), neither of which has any children.
Complete the following method so that it computes the largest sum
that can be achieved using a subset of the numbers in nums
without exceeding goal. For example, if nums
holds 20, 42, and 25, and goal is 50, then the method
would return 45.
Your method will need to be recursive, essentially determining
the sums of all possible subsets of nums. The
index parameter will be 0 with the initial call to
subsetSum, but it will have different values at lower
levels of the recursion. You may add additional parameters as well,
if you think them necessary. (There is a solution using only these
parameters, though.)
public static int subsetSum(int[] nums, int goal, int index) {
if(index == nums.length) {
return 0;
} else {
int with = nums[index] + subsetSum(nums, goal - nums[index], index + 1);
int without = subsetSum(nums, goal, index + 1);
if(with > without) return with;
else return without;
}
}
Suppose we have the ListNode class as defined in the text.
public class ListNode<E> {
private E val;
private ListNode<E> next;
public ListNode(E v, ListNode<E> n) {
val = v; next = n;
}
public E getValue() { return val; }
public ListNode<E> getNext() { return next; }
public void setValue(E v) { value = v; }
public void setNext(ListNode<E> n) { next = n; }
}
head which refers to the first node of a singly
linked list. We already know that head is not
null. Write a program fragment that removes the final
node (i.e., the node with nothing after it) from the list
referenced by head.
if(head.getNext() == null) { // the list contained only one node
head = null;
} else {
ListNode<E> n = head; // n will be the next-to-last node
while(n.getNext().getNext() != null) n = n.getNext();
n.setNext(null);
}
Suppose we have ListNode defined below (repeating the first definition in the text).
public class ListNode<E> {
private E val;
private ListNode<E> next;
public ListNode(E v, ListNode<E> n) {
val = v; next = n;
}
public E getValue() { return val; }
public ListNode<E> getNext() { return next; }
public void setValue(E v) { value = v; }
public void setNext(ListNode<E> n) { next = n; }
}
Suppose, moreover, that we have already begun to implement a class for storing a linked list.
public class MyLinkedList<E> {
private ListNode<E> head;
private ListNode<E> tail;
private int count;
public MyLinkedList() {
head = null;
tail = null;
count = 0;
}
// ...
Write the following instance methods as they should appear within the MyLinkedList class.
E get(int index)Returns the element at index (numbered from 0).
(In both get and add, don't worry about starting
from the tail if it is closer to the requested index.)
E removeFirst()Removes the first value in this list, and returns the value removed (not the node removed).
public E get(int index) {
ListNode<E> cur = head;
for(int i = 0; i < index; i++) {
cur = cur.getNext();
}
return cur.getValue();
}
|
public E removeFirst() {
Value ret = head.getValue();
head = head.getNext();
if(head == null) tail = null;
count--;
return ret;
}
|
Write the following instance methods as they should appear within the MyLinkedList class of the preceding problem.
void add(int index, E val)Inserts val into position index of
this list. (Don't worry about what happens if index is
invalid.)
int indexOf(E val)Returns the index of the first occurrence of val in
this list, or −1 if it doesn't occur in the list at
all.
public void add(int index, E val) {
if(index == 0) {
head = new ListNode<E>(val, head);
if(tail == null) tail = head;
count++;
} else {
ListNode<E> n = head;
for(int i = 0; i < index - 1; i++) {
n = n.getNext();
}
n.setNext(new ListNode<E>(val,
n.getNext()));
if(tail == n) tail = n.getNext();
count++;
}
}
|
public int indexOf(E val) {
int index = 0;
ListNode<E> n = head;
while(n != null) {
if(val == n.getValue()) {
return index;
}
index++;
n = n.getNext();
}
return -1;
}
|
[Incidentally, the indexOf method is a method in the
java.util.List interface similar to the getIndex method
above, but it works slightly differently:
Instead of using == to compare objects, it uses the
equals method defined in the Object class (which is
often overridden by subclasses, including Integer and String).
Thus, the if condition would read
(Actually, the code would
need to be somewhat more complicated so that it works
correctly even if val.equals(n.getValue()).val is null.)]
Suppose x refers to a LinkedList object.
Which of the following two
fragments would be preferred for printing all the elements of
x, and why?
A.
for(int i = 0; i < x.size(); i++) {
String str = x.get(i);
System.out.println(str);
}
|
B.
for(Iterator<String> i = x.iterator(); i.hasNext(); ) {
String str = i.next();
System.out.println(str);
}
|
B. is preferable, because it is faster. Solution
A. uses the get method many times to retrieve
elements from near the middle of the LinkedList, and the LinkedList
will end up scanning through nearly half the list with each such call
to get. The Iterator, however, will remember
its
current location in the list, and each step to the following
element will not require scanning through many other elements
(as in A.).
Explain why an Iterator is preferable for iterating through the elements over a LinkedList (as opposed to accessing elements through repeated requests to LinkedList directly).
It is faster. Using the get method many times, each
get for an element
near the middle of the LinkedList will force the LinkedList to
scan through nearly half the list to find the requested
element. The Iterator, however, will remember
its
current location in the list, and each step to the following
element will not require scanning.
Below, complete sumAll to compute and return
the sum of a
list of Integers, using an Iterator to step through the
values.
public static int sumAll(List<Integer> all) {
public static int sumAll(List<Integer> all) {
int total;
for(Iterator<E> it = all.iterator(); it.hasNext(); ) {
total += it.next().iterator();
}
return total;
}
Convert the following fragment to use an Iterator for iterating
through the strings in names.
int i = 0;
while(i < names.size()) {
if(names.get(i).startsWith("B")) {
names.remove(i);
} else {
i++;
}
}
Iterator<String> it = names.iterator();
while(it.hasNext()) {
String s = it.next();
if(s.startsWith("B")) {
it.remove();
}
}
The below fragment removes any adjacent duplicates from the
List object referenced by data.
Convert the fragment to use an Iterator instead.
int i = 1;
while(i != data.size()) {
if(data.get(i).equals(data.get(i - 1))) {
data.remove(i);
} else {
i++;
}
}
Iterator it = data.iterator();
Object last = it.next();
while(it.hasNext()) {
Object current = it.next();
if(current.equals(last)) {
it.remove();
} else {
last = current;
}
}
Consider the following code fragment using a List variable
data.
for(int i = 0; i < 100; i++) {
data.set(i, new Integer(i));
}
Which of the following applies?
| A. | This is much faster if data is an
ArrayList. |
| B. | This is much faster if data is a
LinkedList. |
| C. | There is not a dramatic difference. |
data is an ArrayList.
Suppose we are writing a program for simulating customer behavior, and we want to include a List to represent a line of customers. The primary operations we want to perform are to add Customer objects onto the end of the list and to remove Customer objects from the front of the list.
As a programmer interested in making sure the simulation runs efficiently, would you suggest that we use a LinkedList or an ArrayList to represent the line — or would you say that it doesn't matter? Explain your reasoning.
The LinkedList would be the better choice. When we remove from the front end of an ArrayList, the ArrayList must shift everything in the list forward a spot, which can consume lots of time if the line ever becomes very long. With the LinkedList, however, adding to the end and removing from the front can both be done without looking at more than one or two nodes of the list.
If you want the functionality of the List interface, and you want to choose the faster option of the ArrayList and LinkedList implementations, how should you decide?
If you want to be able to quickly access elements of the list, you should choose the ArrayList; if, however, you want to be able to remove and add elements on both ends of the List, then the LinkedList will be the more efficient choice.