Write the following Big-O bounds in order, from smallest to largest.
For each of the following mathematical expressions, give the simplest and tightest possible Big-O bound for it.
| a. | 4 + 12 n + 14 n² + n³ |
| b. | 23(ln ln n) + (ln n) + 10(ln n)² |
| c. | (n ln n) + n3/2 + 12000 |
Using big-O notation in terms of the parameter n, how much time does the following method take? Give the tightest possible bound, and explain your answer.
public static int mystery(int n) {
int count = 0;
int cur = 1;
while(cur < n) {
count++;
cur = cur * 2;
}
return cur;
}
The below functions both determine
mn without using
Math.pow.
a.
int pow(int m, int n) {
int ret = 1;
for(int i = 0; i < n; i++) {
ret *= m;
}
return ret;
}
| b.
int pow(int m, int n) {
int ret = 1;
int k = m;
int i = n;
while(i > 0) {
if(i % 2 == 1) ret *= k;
k *= k;
i /= 2;
}
return ret;
}
|
Using big-O notation in terms of n, how much time
does each take?
Provide the tightest bound that you can.
Consider the following method, which finds and removes all duplicated numbers in the parameter array. Note that the method has three loops.
public static int removeDuplicates(char[] arr) {
int len = arr.length;
int i = 0; // index of current item to find
while(i < len) {
int j; // will be index of duplicate of arr[i]
for(j = i + 1; j < len; j++) {
if(arr[i] == arr[j]) break;
}
if(j == len) { // no duplicate of arr[i] found; go to next i
i++;
} else { // duplicate found; shift array over arr[j]
for(int k = j + 1; k < len; k++) {
arr[k - 1] = arr[k];
}
len--;
arr[len] = 0;
}
}
return len;
}
Let n represent the length of arr.
In terms of n, how much time does
the above method take? Use Big-O notation to express your answer, and
provide the tightest bound that you can.
In terms of the variable n, how much time does the below
program fragment take?
Give your answer using Big-O notation, and give the
tightest and simplest bound possible. Justify your answer.
int i = 1;
int j = 0;
while(i < n) {
j++;
if(j == i) {
i++;
j = 0;
}
}
Consider the following method.
public static int mystery(int n) {
int j = 0;
for(int i = 0; j <= n; i++) {
j += 2 * i + 1;
}
return i - 1;
}
In terms of the input n, what is the tightest big-O bound you can give on the running time of the above method? Describe the reasoning underlying your answer.
Using big-O notation in terms of its parameter n, what is the running time of the below program fragment? Give the smallest bound that you can, and justify your answer.
int total = 0;
for(int i = 1; i < n; i++) {
int k = 1;
while(k < i) { k = k + k; }
while(k > 1) { k /= 2; total++; }
}
System.out.println(total);
Consider the following method that finds the smallest factor above 1 for a given number n, without using any division or multiplication. (A factor for a number n is an integer that divides into n exactly. For example, the factors of 45 are 1, 3, 5, 9, 15, and 45.)
public static int findFactor(int n) {
int i = 1;
int j = n - 1;
int p = j; // invariant: p = i * j
while(p != n && i < j) {
i++; p += j;
while(p > n) { j--; p -= i; }
}
return p == n ? i : n;
}
How much time does this method take? Give your answer using Big-O notation in terms of n, and give the tightest and simplest bound possible. Justify your answer.
Using big-O notation in terms of its parameter n, what is the running time of the below program fragment? Give the smallest bound that you can, and justify your answer.
int total = 0;
for(int i = 1; i < n; i *= 2) {
for(int j = i; j < 2 * i; j++) {
total += j;
}
}
System.out.println(total);
The following method determines whether the parameter array of
booleans contains at least two true values.
In terms of n, the length of the parameter array, how much time does
this method take? Give your answer using Big-O notation, and give the
tightest and simplest bound possible. Justify your
answer.
public static int findTruePair(boolean[] flags) {
int n = flags.length;
for(int i = 0; i < n; i++) {
if(flags[i]) {
for(int j = i + 1; j < n; j++) {
if(flags[j]) return true;
}
}
}
return false;
}
Complete the below method so that it implements insertion sort.
public static void sort(int[] nums) {
Suppose you wanted to find the largest 10 numbers in an array with no duplicated numbers. Describe an efficient algorithm to do this, and say how much time it would take in terms of n, the array length.
Let n represent the length of the following method's
nums parameter. In terms of
n, how much time does the method take? Use Big-O
notation to express your answer, and provide the tightest bound that
you can. Justify your answer.
public static void sortBadly(double[] nums) {
for(int i = 0; i < nums.length; i++) {
double item = nums[i];
int k = 0;
while(nums[k] < item) k++;
for(int j = i; j > k; j--) nums[j] = nums[j - 1];
nums[k] = item;
}
}
Suppose that instead of an array of integers to sort, you have a linked list. In terms of Big-O notation, how much time would Mergesort take for this list? Explain your reasoning.
In your own words, describe how the Quicksort algorithm works.
Suppose we are told to sort the array <1,4,5,8,3,2,7,6> using Quicksort, using the first number of the array segment to be sorted as the pivot each time. Draw the recursion tree. (The base case is when the array segment has zero or one elements.)
Both Mergesort and Quicksort are O(n log n) algorithms. In general, though, which is faster, and why does it turn out to be faster?
Consider the following two techniques for finding the mode (i.e., the value occurring most often) in a sequence of integer test scores between 0 and 100.
(A.) Insert each value into an array so that the array is always in increasing order. Then go through array and determine the longest
runof equal numbers.int[] nums = new int[n + 1]; for(int i = 0; i < n; i++) { int value = in.nextInt(); int j = i - 1; while(j >= 0 && value[j] > value) { nums[j + 1] = nums[j]; j--; } nums[j] = value; } int curValue = nums[0]; int curRun = 1; int modeValue = lastValue; int modeRun = lastRun; for(int i = 1; i < n; i++) { if(nums[i] == curValue) { curRun++; if(curRun > modeRun) { modeValue = curValue; modeRun = curRun; } } else { curValue = nums[i]; curRun = 0; } } System.out.println(modeValue);(B.) Create a second array,
count, that tracks how many times each score appears as we first go through the numbers of the array. Then go throughcountto determine the index of its largest value, which will be the mode.int[] count = new int[101]; for(int i = 0; i < n; i++) { int value = in.nextInt(); count[value]++; } int max = 0; for(int i = 1; i < count.length; i++) { if(count[i] > count[max]) max = i; } System.out.println(max);
For each of the following, give your answer using Big-O notation in terms of n, the number of scores in the sequence, and give the tightest and simplest bounds possible.
a. How much time does each technique take?
b. How much memory does each technique take?
Suppose we have a city map with n intersections,
each assigned a different integer between 0 and n − 1.
Suppose, moreover, that we have a connected method
that takes the numbers representing two intersections and says whether
there is a road between them.
We want to write a method hasPath that takes the numbers of two
intersections, s and t, and a length k, and determines whether
there is a path from s to t going along no more than k
roads. We have two techniques for doing this.
|
(A.) For each point adjacent to s, we see whether there is a path of length k − 1 from that point to t.
boolean hasPathA(int s, int t, int k) {
if(s == t) return true;
else if(k == 0) return false;
else if(k == 1) return connected(s, t);
for(int i = 0; i < n; i++) {
if(connected(s, i)
&& hasPathA(i, t, k - 1)) {
return true;
}
}
return false;
}
|
(B.) For each of the n points, we look for a path from s to that point of length at most k / 2, and a path from there to t of length at most k / 2.
boolean hasPathB(int s, int t, int k) {
if(s == t) return true;
else if(k == 0) return false;
else if(k == 1) return connected(s, t);
int half = k / 2;
for(int i = 0; i < n; i++) {
if(hasPathB(s, i, half)
&& hasPathB(i, t, k - half)) {
return true;
}
}
return false;
}
|
How much memory does each technique take? Give your answer using Big-O notation in terms of n, and give the tightest and simplest bound possible. Justify your answers.
(Recall that each recursive call in execution at the same time requires its own memory. If each recursive call takes m memory, and the recursion tree has height h, then the overall recursion requires O(h m) space.)
O(1), O((log n)²), O(n), O(n log n), O(n sqrt(n)), O(n²), O(2n)
| a. | O(n³) |
| b. | O((log n)²) |
| c. | O(n3/2) |
It takes O(log n) time. Since cur doubles with each
iteration of the loop, after going through the loop k times,
cur will be 2k. After going through the loop log2 n
times, cur will be
2log2 n,
or n, and we will stop.
Thus, there are O(log n) iterations of the loop; since each iteration
takes O(1) time, the total time consumed is
O(log n).
| a. | O(n) |
| b. | O(log n) |
It takes O(n²) time. We go through the
loop once when i is 0, twice when i is
1, three times when i is 2, three times when
i is 2, and so on. We stop by the time i reaches
n; so the question is: What is
1 + 2 + 3 + … + n?
This summation is
n (n + 1) / 2
= (1/2) n² + (1/2) n
= O(n²).
It takes O(sqrt(n)) time. In fact, the function computes the largest integer that is at most sqrt(n). You can see that it does this by observing that the loop maintains an invariant of j = i². (After all, if j = i² at the beginning of an iteration, then during the iteration, j becomes j + 2 i + 1 = i² + 2 i + 1 = (i + 1)².) Since i goes up by 1 each iteration, and it stops once it passes sqrt(n), there are at most 1 + sqrt(n) iterations.
(You may be tempted to use reasoning that is less formal than the above, perhaps pointing to examples that you have run. This is only a partial answer, as the reasoning is not mathematically sound. But it at least provides some evidence.)
O(n log n): For each i value, each inner loop has approximately log2 i iterations — the first one starting at 1 and doubling until we reach i, and the second one halving until we reach 1 again. Thus, the total time per iteration of the outer loop is O(log i + log i) = O(2 log i) = O(log i) = O(log n). (The last step comes from the fact that i ≤ n.) The outer loop has n iterations, so the total time is O(n log n).
An answer of O(n sqrt(n)) would be partially acceptable. The reasoning: As we go through the loop, j always decreases to a number less than n / i, and so once i reaches sqrt(n), n / i will be less than that, and the method stops. Thus, there are at most sqrt(n) iterations of the outer loop. For each iteration, j may have to decrease significantly, but it won't decrease for more than n iterations, so O(n sqrt(n)) is a valid answer.
It is possible, however, to derive a better bound by observing that the total number of iterations of inner loop, across the entire method execution, will be less than n, since j starts at n − 1, decrements each time through the inner loop, and stops once it reaches sqrt(n). Thus, the total time spent on the inner loop over the entire execution is O(n), and the total time spent on the outer loop (but not including time for the inner loop) is O(sqrt(n)); thus, the total time overall is O(sqrt(n) + n) = O(n).
A first-cut solution, which would be acceptable at this level,
would be O(n log n): The
reasoning would be that the outer loop has log2 n iterations since
i starts at 1 and doubles with each iteration until it
reaches n, and log2 n doublings will accomplish this,
while the inner loop has at most 2 n iterations, since
j starts at i, which is at least 1, and stops
at 2 i, which is less than 2 n since i is less
than n. Thus we have
O((log2 n) 2 n)
= O(n log n)
time.
An answer of O(n) is also possible. The reasoning is this:
The inner loop will execute only once the first time through the
outer loop (when i is 1),
twice on the second outer iteration (when i is 2),
four times on the third outer iteration (when i is 4),
and so on. Thus, the total number of iterations of the inner
loop, across all iterations of the outer loop,
is
1 + 2 + 4 + 8 + … + n
= 2 n - 1,
and so the total time
spent on the inner loop is O(n). If we ignore the inner loop,
the total time spent on the outer loop is O(log n),
so the total time overall is
O(n + log n)
= O(n).
O(n).
If flags contains
no true values, then the inner loop will never
execute, so every iteration of the outer loop takes
O(1) time, for a total of O(n)
time.
If flags contains
one true value, then the inner loop will be
reached only once, adding an additional
O(n)
to the above, for a total still of O(n).
And if flags contains two or more true
values, then the inner loop will still be reached only once
(since the one time the inner loop is executed, the method will
return), for a total of
O(n) time. So in any of these cases, the
amount of time is
O(n).
for(int i = 1; i < nums.length; i++) {
int t = nums[i];
int j = i - 1;
while(j >= 0 && t < nums[j]) {
nums[j + 1] = nums[j];
j--;
}
nums[j + 1] = t;
}
}
The easiest algorithm is one similar to selection sort: We find the largest number (taking O(n) time), then we find the largest number that is less that one (taking another O(n) time), then the largest number less than that one, and so on, for ten iterations. The total amount of time is 10 ⋅ O(n) = O(n).
O(n²). Each iteration of the outer loop takes O(n) time, since it contains two loops, one after the other, each taking O(n) time. (These loops iterate through at most n items, and they take O(1) time per iteration.) There are n − 1 iterations of the outer loop, so the total time is O((n − 1) ⋅ n) = O(n²).
It would still take O(n log n) time. Dividing the list into two pieces is somewhat harder with an array (where we simply went straight to the middle of the array), but even with a list this is just a matter of going through and putting one node into one list, the next node into the other — an O(n) process. Then we have our two recursive calls (just as with the array), and then merging the two n / 2-length lists would be very similar to what we saw with the array, taking O(n) time. The non-recursion overhead is still O(n) so the total time is O(n log n).
Given an array to sort, we choose a pivot
number (typically
through randomly selecting one of the numbers in the list) and
partition the elements so that all numbers less than or equal to
the pivot come at the beginning of the array, and all numbers
greater than it come at the end of the array.
We then recursively sort the two subsegments resulting from the
partitioning.
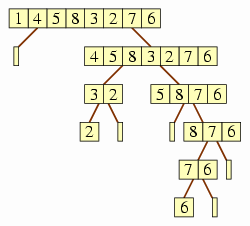
At the root is <1,4,5,8,3,2,7,6>, whose children are an empty array (with no children) and <4,5,8,3,2,7>. The latter has two children, labeled <3,2> and <5,8,7,6>. The node labeled <3,2> has a child containing <2> alone and another child containing nothing; neither of these has any children. the node labeled <5,8,7,6> has a child containing nothing (with no children) and another containing <8,7,6>. The latter has two children, the first containing <7,6> and the second containing nothing. The latter of these has no children, but the former has children containing 6 alone and another containing nothing; neither of these has any further children.
Quicksort turns out to be faster because its implementation does not require that numbers be copied between locations nearly as often. Mergesort essentially requires that all numbers be copied during the merge process of each recursive call, and the resulting copying process makes it less efficient.
a. (A.) takes O(n²) time; (B.) takes O(n) time.
b. (A.) takes O(n) space; (B.) takes O(1) space.
[In fact, there is nothing to recommend (A.) based on its Big-O bounds.]
(A.)'s recursion tree has a height of n, and each level of the recursion takes O(1) space, for a total of O(n) space.
(B.)'s recursion tree has a height of log2 n, and each level of the recursion takes O(1) space, for a total of O(log n) space.