Section 6.1:
[1]
[2]
[3]
Section 6.2:
[1]
[2]
[3]
[4]
[5]
[6]
Section 6.3:
[1]
[2]
[3]
Using Java's syntax for defining interfaces, define the Map
interface as it exists in the java.util package. Your
definition should include at least 5 of the 6 methods we saw in
class.
public interface Map<K,V> {
public E get(K key);
public E put(K key, V value);
public E remove(K key);
public boolean containsKey(K key);
public int size();
public Set<K> keySet();
}
Suppose we have a Map object mapping student names to test scores. Complete the following method so that it would return the name of the student with the highest test score. (If there is a tie, it doesn't matter which of the top-scoring students you return. You can assume that there is at least one score in the map.)
public static String findTopStudent(Map<String,Integer> scores) {
int maxScore = Integer.MIN_VALUE;
String maxName = null;
for(Iterator<String> names = scores.keySet().iterator(); it.hasNext(); ) {
String name = names.next();
int score = scores.get(name).intValue();
if(score >= maxScore) {
maxName = name;
maxScore = score;
}
}
return maxName;
}
Define a class named Catalog whose instances represent assignments of prices to book titles. Your definition should store the price assignments using a TreeMap (or HashMap), and it should define the following instance methods.
Catalog(double defaultPrice)(Constructor method) Constructs a catalog where all books are
assumed to cost defaultPrice.
void setPrice(String item, double price)Assigns price to item. Note that
item may or may not already have a price assigned to it;
if it had a price previously, this method would change this
price.
double getPrice(String item)Returns the price currently associated with item. If
there is no price associated with the book (i.e.,
setPrice has not been invoked with item as a
parameter), the method should return the default price given
to the constructor.
The following method illustrates how another class might use your Catalog class.
public static void run() {
Catalog prices = new Catalog(30);
prices.setPrice("Iliad", 50);
prices.setPrice("Huck Finn", 20);
prices.setPrice("Iliad", 40);
System.out.println(prices.getPrice("Iliad")) // prints "40"
System.out.println(prices.getPrice("Moby Dick")); // prints "30"
}
public class Catalog {
private TreeMap<String,Double> prices;
private double defaultPrice;
public Catalog(double defaultPrice) {
this.defaultPrice = defaultPrice;
prices = new HashMap<String,Double>();
}
public void setPrice(String item, double price) {
prices.put(name, new Double(price));
}
public double getPrice(String item) {
if(prices.containsKey(item)) return prices.get(item).doubleValue();
else return defaultPrice;
}
}
Suppose we have a hash table of size 10 and we are adding Integers (whose hash code method simply returns the integer represented). How will the hash table appear after the primes less than 50 are inserted into it?
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47

(The order of the numbers within each bucket is not important.)
[Bucket 0 is empty. Bucket 1 contains 11, 31, 41. Bucket 2 contains 2. Bucket 3 contains 3, 13, 23, 43. Bucket 4 is empty. Bucket 5 contains 5. Bucket 6 is empty. Bucket 7 contains 7, 17, 27, 47. Bucket 8 is empty. Bucket 9 contains 19, 29.]
Suppose we have a five-bucket hash table for storing strings; each string's hash code is simply the length of the string. Diagram the hash table at it would appear after adding the following strings.
ab, abbot, abdomen, abecedarian, abhors
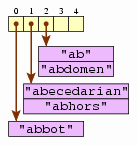
(The order of the strings within each bucket is not important.)
[Bucket 0 contains abbot. Bucket 1 contains abecedarian and abhors. Bucket 2 contains ab and abdomen.]
Identify a data structure invariant maintained in the hash table data structure. Your invariant should describe the relation between the array and the keys stored within the table.
Here are two possible answers:
For each key in the hash table, that key can be found in the
bucket at the index key.hashCode() (after this hash code
is mapped into the range of the array).
For any entry in any bucket, the key-value pair in that
entry reflects the
key-value pair submitted via a call to put in the
past.
Contrast the relative advantages of using a TreeSet versus a HashSet. In what situations is a HashSet the better choice for storing a Set, and in what situations is a TreeSet a better choice?
A hash table is the faster of the two (providing O(1) time for all operations assuming a good hash function); a binary search tree is slower (O(log n) for all operations), but it has the virtue of keeping data in sorted order. Thus, if iterating efficiently through items in increasing order is a priority, then TreeSet is the better choice; otherwise, HashSet is.
Describe step-by-step the process used to accomplish
the get operation in the hash table implementation of
the Map ADT. You may describe your process in Java, in
English, or a mix of both.
We first apply the hash function to the key to retrieve an
integer, and then we determine the remainder when this integer
is divided by the table's length. We look at this index within
the table to retrieve a linked list there — the bucket.
We
step through each entry in the bucket to see whether the key is
in that entry; if we find the key, we return the value associated
with the key in that entry. If we do not find the key, we return
null.
Suppose we already have the Entry class as shown below.
class Entry<K,V> {
private K key;
private V value;
private Entry<K,V> next;
public Entry(K k, V v) { key = k; value = v; }
public K getKey() { return key; }
public V getValue() { return value; }
public void setValue(V v) { value = v; }
public Entry<K,V> getNext() { return next; }
public void setNext(Entry<K,V> v) { next = v; }
}
We are now writing our own version of Java's built-in
HashMap class, with the below code so far. Complete the
get method.
public class MyHashMap<K,V> implements Map<K,V> {
private Entry<K,V>[] table;
public HashMap() {
table = (Entry<K,V>[]) new Entry[13];
}
public V get(K key) {
int index = value.hashCode() % table.length;
if(index < 0) index = -index;
for(Entry<K,V> n = table[index]; n != null; n = n.getNext()) {
if(n.getKey().equals(key)) return n.getValue();
}
return null;
}
In an earlier question, we hashed all the primes less than 50 into a 10-bucket hash table, and the hash code function (the remainder modulo 10) worked fairly poorly. Make up a hash code function that works better for the same set of numbers, draw the hash table after hashing all the numbers, and explain why you think this distribution is better than for the previous answer.
Of course, there are lots of good answers. Here's my solution, in which we basically add the ten's digit to the number to arrive at the hash code.
int hashCode() { return intValue() + intValue() / 10; }

[Bucket 0 contains 19 and 37. Bucket 1 contains 29 and 47. Bucket 2 contains 2 and 11. Bucket 3 contains 3. Bucket 4 contains 13 and 31. Bucket 5 contains 5, 23, and 41. Bucket 6 is empty. Bucket 7 contains 7 and 43. Bucket 8 contains 17. Bucket 9 is empty.]
This solution reduces the number of large buckets: Whereas before there were two buckets with four elements and one bucket with three elements, with this hash function there are no buckets with four or more elements and only two with three elements.
Suppose that we have the following City class, and we
want to modify it so that we can use a HashSet<City>.
Note that two cities with the same city name and state name
should appear in the HashSet only once; note also that
the mayor of a City may change while the City
is in the HashSet.
Add the necessary additional methods into the class that it
supports being inside a HashSet.
public class City {
private String name;
private String state;
private String mayor;
public City(String n, String s, String m) { name = n; state = s; mayor = m; }
public void setMayor(String value) { mayor = value; }
public boolean equals(Object other) {
if(!(other instanceof City)) return false;
City c = (City) other;
return c.name.equals(this.name) && c.state.equals(this.state);
}
public int hashCode() {
return 31 * city.hashCode() + state.hashCode();
}
[The hashCode method should certainly not refer to
the mayor instance variable, since it may change
after the city is added into the HashSet.]
Suppose we know our hash function will give us a number between 0
and MAX.
In class, we mapped this into a valid index of our array using
the remainder (modulus) operator `%'.
index = key.hashCode() % table.length;
The following is an alternative way to map integers to indices in the array.
index = (int) ( (((double) key.hashCode()) / MAX) * table.length);
Both map hash codes into valid indices for table.
Neglecting concerns about the computational efficiency, which is
likely to work better, and why?
The first technique (finding the remainder) is likely to work better. The second technique will tend to map hash codes which are close to each other into the same bucket. For example, if we have a number of values whose hash codes tend to be small (between 0 and 100), then everything would map into index 0.
[If being able to iterate through keys in order of their hash code is useful, the second technique has some usefulness. However, this isn't very likely to be desirable.]