[1] [2] [3] [4] [5] [6] [7] [8] [9] [10]
[8 pts]
Give an invariant for the below loop that allows for the
conclusion that after the loop, the ArrayList
a contains no adjacent duplicates.
int i = 1;
while(i < a.size()) {
if(a.get(i).equals(a.get(i - 1))) {
a.remove(i);
} else {
i++;
}
}
There are no adjacent duplicates among the first
i elements of a.
[8 pts]
In terms of n, how much time does the code fragment at
right take? Give your answer using
Big-O notation, with the tightest and simplest bound possible. Justify
your answer.
int i = 0;
int j = 1;
while(j < n) {
i++;
if(i == n) {
j *= 2;
i = 0;
}
}
O(n log n).
Every n iterations of this loop, i
finally reaches n and then j
doubles. Starting from 1, j can double itself
1 + log n times before reaching
21 + log n = 2 n.
Thus, there are at most
n log n iterations,
and each iteration takes O(1) time,
for a total of
O(n log n) time.
[4 pts] Write the in-order traversal of the below tree.
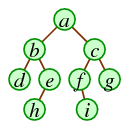
d b h e a f i c g
[10 pts]
We have started to write an implementation of the Set
interface below using a binary search tree. Complete the
contains method.
public class BstSet<E> implements Set<E> {
private TreeNode<E> root;
private int curSize;
public BstSet() { root = null; curSize = 0; }
public boolean contains(E value) {
Comparable<E> comp = (Comparable<E>) value;
TreeNode<E> n = root;
while(n != null) {
int c = comp.compareTo(n.getValue());
if(c < 0) {
n = n.getLeft();
} else if(c > 0) {
n = n.getRight();
} else {
return true;
}
}
return false;
}
[10 pts]
Suppose we are implementing the Map interface using a
hash table. Describe step-by-step in detail how the get
method would work.
It applies the hashCode method to the
requested key and maps this int into a valid
array index by finding the remainder of dividing the hash code
by the array length.
It goes to that array index to find the first entry of a bucket. It steps through each entry of the bucket until it finds an entry whose key matches the requested key.
If it finds such an entry, it returns the value stored
within that entry; and if it doesn't find such an entry, the method
returns null.
[8 pts]
Explain why we say that HashMap's get method
takes O(1) time.
The hashCode method is generally quite quick,
and certainly independent of the number of things in the map,
so it makes sense to say that mapping the requested key to
an array index takes O(1) time.
The get method must also step through each
entry in its bucket. A reasonably good hashCode
method will distribute the keys largely evenly among the
buckets, and the HashMap class is written
so that the average bucket length is 0.75.
(It doubles the array length whenever the average bucket
length exceeds 0.75). As a result, we end up stepping through
only 0.75 entries in the bucket, on average.
[8 pts]
Suppose we have a class PhoneNumber class for representing
phone numbers. Each instance has int instance variables,
exch for the 3-digit exchange and ext
for the 4-digit extension. For example, the number
450-1377 has an exchange of 450 with an extension
of 1377.
Critique each of the following hashCode
methods.
| a. |
int hashCode() {
return exch;
}
|
| b. |
static Random rand = new Random();
int hashCode() {
// returns random integer from -2^31 to 2^31-1
return rand.nextInt();
}
|
a. This method leads to many collisions if we have several telephone numbers in the same exchange, as is likely if we are storing telephone numbers from the same town.
b. This method returns a different value each time
it is invoked. Consequently, if we use hashCode
to add a value into a HashSet and we later use
contains on the same value, we'll get a different
hash code, and so the HashSet will look in a
different bucket than when the value was stored.
[8 pts] Describe how the Stack and Queue ADTs are functionally different.
With a stack, additions and removals both occur at the same end of a list of stored elements. With a queue, they occur on opposite ends.
[8 pts]
How can the Queue ADT be implemented so that both add
and remove take O(1) time using an array to hold
the queue's elements?
We use a circular buffer,
where both the front and
the rear of the queue shift — the rear index shifts on
an add, and the front index shifts on a
remove. When either goes off the end of the array,
it wraps around
back to index 0.
[8 pts]
Suppose that Comparable is an interface and
Integer is an implementation of that interface.
Suppose, moreover, that ZERO is an Integer
constant defined within the class we are writing.
For each of the following fragments, would it compile as written? (At least one of them would.) For each of the other(s), explain how you could repair it so it would compile.
| a. |
boolean isNeg(Comparable a) {
return a.compareTo(ZERO) < 0;
}
void run() {
Comparable a = new Comparable(0);
System.out.println(isNeg(a));
}
| b. |
boolean isNeg(Comparable a) {
return a.compareTo(ZERO) < 0;
}
void run() {
Comparable a = new Integer(0);
System.out.println(isNeg(a));
}
| |
| c. |
boolean isNeg(Integer a) {
return a.compareTo(ZERO) < 0;
}
void run() {
Comparable a = new Comparable(0);
System.out.println(isNeg(a));
}
| d. |
boolean isNeg(Integer a) {
return a.compareTo(ZERO) < 0;
}
void run() {
Comparable a = new Integer(0);
System.out.println(isNeg(a));
}
|
a. This is illegal because it is not legal to
create an instance of an interface as in
.new Comparable(0)
b. This is legal.
c. This is illegal because it is not legal to
create an instance of an interface as in
.
Moreover, we cannot pass a new Comparable(0)Comparable as an
argument to a method that expects an Integer
parameter.
d. This is illegal because we cannot
pass a Comparable as an
argument to a method that expects an Integer
parameter.