L1.1.
For each of the following circuits, write
a truth table tabulating the circuit's output for each combination of
inputs.
| a. |

|
| b. |

|
L2.1.
For the following circuit, write the Boolean expression that
most closely corresponds to the circuit.

L2.2.
For each of the following Boolean expressions,
draw the logic circuit corresponding most closely to it.
| a. |
x + y + x |
| b. |
x y + x y |
L2.3.
For each of the following Boolean expressions,
draw the logic circuit corresponding most closely to it.
| a. |
w x + x y |
| b. |
x (y z + y z) |
L2.4.
For each of the following Boolean expressions, write
a truth table tabulating the expression's value
for each combination of variable values.
| a. |
x + x + y |
| b. |
x y + x + z |
L2.5.
Consider the following C statement.
if (!(a < b && b < c)) between = 0;
a. Rewrite the if condition to an
equivalent condition without using the NOT operator !.
b. What is the name of the Boolean algebra law that this
illustrates?
L2.6.
For each of the following,
what is the equivalent two-operator Boolean expression
according to DeMorgan's laws?
a. x y without “multiplication”
b. x + y without “addition”
L2.7.
For each of the following, draw a smaller circuit (i.e., fewer gates)
accomplishing the same task as the circuit given.
| a. |

|
| b. |

|
|
L2.8.
What is the unminimized sum-of-products expression for the
following truth tables? (Use multiplication for AND, addition for
OR.)
| a. |
| b. |
| c. |
| x | y | z | out |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
|
L2.9.
For the following truth table,
write the unminimized sum-of-products expression
and draw the corresponding circuit.
| x | y | z | out |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
L2.10.
Using AND, OR, and NOT gates, design a circuit
that takes three inputs i3, i2, and i1 and
two outputs p1 p0
that are 11 (that is, both p1 and p0 are 1) when i3 is 1,
10 (p1 is 1, p0 is 0) when i3 is 0 but i2 is 1,
01 when i3 and i2 are 0 but i1 is 1,
and 00 when all inputs are 0.
(Incidentally, a component like this — computing the first 1 among
an ordered list of inputs — is called a priority encoder.)
| i3 | i2 | i1 | p1 | p0 |
| 1 | x | x | 1 | 1 |
| 0 | 1 | x | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
L3.1.
What is the depth of the following circuit?

L3.2.
Given the below Karnaugh map, identify the corresponding minimized
Boolean expression.

L3.3.
Draw a Karnaugh map corresponding to the following truth table,
and derive a minimized Boolean expression for the function.
| x | y | z | out |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
L3.4.
Draw a Karnaugh map corresponding to each of the following truth
tables, and derive a minimized Boolean expression for the function
for each.
| a. |
| x | y | z | out |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| b. |
| x | y | z | out |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
|
L3.5.
The following truth table computes the 2's bit of the product of
two 2-bit inputs. Draw a Karnaugh map and indicate a
minimized sum-of-products expression corresponding to the
Karnaugh map. (You do not need to draw the circuit.)
| x1 |
x0 |
y1 |
y0 |
p1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
|
|
| x1 |
x0 |
y1 |
y0 |
p1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
|
L3.6.
Design a circuit with three inputs, and which
outputs 1 precisely when at least two of the inputs are 1.
(You'll want to draw a Karnaugh map and to derive a circuit
from that.)
Review L: Logic & circuits: Solutions
L1.1.
| a. |
| | b. |
| x | y | z | out |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
|
L2.1.
(x + y) x
L2.2.
| a. |

|
| b. |
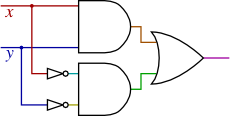
|
L2.3.
| a. |
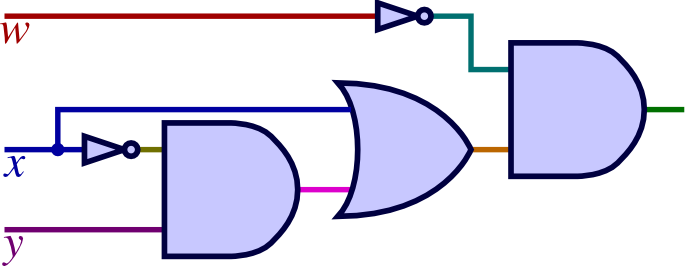 |
| b. |
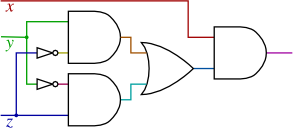 |
L2.4.
| a. |
| b. |
| x | y | z | out |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
|
L2.5.
a. if (a >= b || b >= c) between = 0;
b. DeMorgan's law
L2.6.
L2.7.
| a. |
This involves an application of DeMorgan's
law
x y = x + y.

|
| b. |
This involves an application of the distributive law
x y + x z = x (y + z).

|
L2.8.
| a. |
x y
+ x y |
| b. |
x y
+ x y
+ x y |
| c. |
x y z
+ x y z
+ x y z |
L2.9.
The unminimized sum-of-products expression is
x y z + x y z.

L2.10.
L3.1.
3 (The path from x or y through the OR
gate, NOT gate, and AND gate goes through three gates. There is
another path from x just through the NOT and AND
gates, but it is shorter.)
L3.2.

w x y + x z + x y
L3.3.

The resulting expression is
x z
+ y z
+ x y z.
L3.4.
| a. |
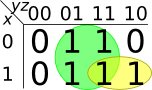
The resulting expression is
z + x y.
|
| b. |

The resulting expression is
z + x y.
|
L3.5.

x1 y1 y0 + x1 x0 y0 + x1 x0 y1 + x0 y1 y0
L3.6.
| Truth table: |
| a | b | c | out |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
|
| Karnaugh map: |

|
| Boolean expression: |
Output is
a b + a c + b c
|
| Circuit: |

|






















