Section 8.1:
[1]
[2]
[3]
[4]
Section 8.2:
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
Section 8.3:
[1]
Section 8.4:
[1]
[2]
[3]
[4]
[5]
Name and briefly describe each of the major operations in the PQueue ADT.
The two crucial operations are add to insert a
value into the collection, and remove to remove the
highest-priority value currently in the collection. (The Priority
Queue ADT also includes two useful but less crucial methods:
isEmpty to query whether the collection currently holds
any values and peek to query what the highest-priority
value currently is.)
Suppose we are using an ordered array to store a priority queue, stored in descending order. Using Big-O notation in terms of the current priority queue's size n, what is the tightest possible bound for each of the following operations? Explain your answers.
addremoveadd would take O(n) time because to
maintain the invariant of ordering, we may have to shift nearly all
the elements in the array to make room for the inserted value.remove would take O(1) time, because
we simply remove the last element of the array. We do not need to do
anything with the other n − 1
elements.Suppose we have an implementation of the PQueue
interface called PQImpl, with a no-arguments constructor
method creating an empty priority queue. Complete the following
class method so that it uses a PQImpl object to put the elements of
the array in sorted order.
public static void sort(String[] data) {
PQueue<String> q = new PQImpl<String>();
for(int i = 0; i < data.length; i++) q.add(data[i]);
for(int i = 0; i < data.length; i++) data[i] = q.remove();
}
Suppose you are to implement the PQueue
interface using an array, where the array is stored in arbitrary
order. That is, we do not maintain the invariant that the array
is in descending order, and in fact methods can reorder
the elements if convenient. The following is a start to the
implementation; complete the remove method. (And don't
bother writing the peek method.)
public class ArrayPQueue<E> implements PQueue<E> {
private E[] elements;
private int numElements;
public ArrayPQueue(int capacity) {
elements = (E[]) new Object[capacity];
numElements = 0;
}
public boolean isEmpty() {
return numElements == 0;
}
public void add(E value) {
elements[numElements] = value;
numElements++;
}
public E remove() {
// remember to raise NoSuchElementException if queue is empty.
if(numElements == 0) throw new NoSuchElementException();
E min = elements[0];
int minPos = 0;
for(int i = 1; i < numElements; i++) {
E t = elements[i];
if(t.compareTo(ret) < 0) { min = t; minPos = i; }
}
numElements--;
elements[minPos] = elements[numElements];
return min;
}
Identify the data structure invariants that describe the structure of a heap. (We identified two in class; you should describe both for full credit.)
The heap must be a full tree. That is, every node above the bottom two levels should have two children, and all the bottom-level leaves should be crowded onto the left side of the level.
For each node of the heap, the node's priority should be less than (i.e., be higher-priority than) its children's priorities.
Suppose we insert 3 into the heap whose tree diagram is below. What will its tree diagram then be?

Suppose we insert 20 into the heap whose tree diagram is below. What will its tree diagram then be?
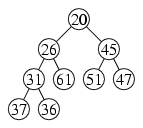
Suppose we remove the minimum from the heap whose tree diagram is below. What will its tree diagram then be?
Suppose we remove the minimum twice from the heap whose tree diagram is below. What will its tree diagram then be?
| after one removal: |  |
| after two removals: |  |
How much time does the add operation take for a heap?
Use big-O notation in terms of the number of values n in the heap.
Explain your answer.
Draw the array representation of a heap whose tree diagram is as follows.
Suppose we have an array whose contents represent a heap, and
suppose i is an index an array element/heap node n.
Give a Java arithmetic expression representing each of the
following.
| a. | the index of n's left child |
| b. | the index of n's right child |
| c. | the index of n's parent |
| a. | 2 * i + 1 |
| b. | 2 * i + 2 |
| c. | (i - 1) / 2 |
[Some people using heaps choose to place the root element at
index 1 rather than 0 as we have done. For them, the answers
would be
2 * i,
2 * i + 1, and
i / 2. I would grade either set of
answers as correct, as long they are consistent with each other.]
Suppose we have a heap of integers stored in an array as follows.
What would the array contain after a single remove
operation?
Suppose we have the following array representing a heap as seen in class (where lower numbers represent higher-priority elements). What will the array contain following an insertion of the number 4 into the heap?
How does heapsort compare to quicksort in terms of big-O efficiency? And how do they compare in practice?
Both are O(n log n). In practice, heapsort is slower than quicksort, since it moves values within the heap more often than quicksort does. (Since their big-O bounds are identical, it's only slower by a constant factor.)
Write Dijkstra's algorithm using pseudocode. That is, you should write it in something resembling code, but you can use English words to describe the individual steps.
Let known be empty.
Let fringe contain the element (Conway, 0) only.
while Mountain Home ∉ known, do:
Remove city c with smallest distance d from fringe.
if c ∉ known, then:
Add (c, d) to known.
for each neighbor b of c, do:
if b ∉ known, then:
Let x be distance from c to b.
Add (b, d + x) to fringe.
Suppose we implement Dijkstra's algorithm so that we add a neighbor
into the priority queue only when the neighbor has not already
been visited.
Run this algorithm to find the shortest path from the gray
node to the black node on the graph below, and number each
edge (road) as it is processed (beginning with
1.
).
[There is a tie in choosing between the fourth and fifth edge. The answer reversing the order of these two edges is also correct.]

Suppose we run Dijkstra's algorithm to find the shortest path
from the gray node to the black node in the map at right.
Number each node (beginning with 1.
for the first
node removed from the priority queue).


Use A* search to determine the shortest route from Clinton to Mountain Home using the map at right. For your heuristic, use the straight-line distance (as the crow flies) from each town to Mountain Home, as follows.
52 Clinton 86 Conway 63 Heber Springs 0 Mountain Home 36 Mountain View 34 Pindall 19 Yellville
Write down the towns in the order they are added to the priority queue. (You need not add towns into the queue if they have already been visited.) When the algorithm visits a town, cross it out and place a number next to it indicating the order in which towns are visited.

| d + h | h | town | order |
| 52 | 0 | 1. | |
| 74 | 38 | 2. | |
| 82 | 48 | 3. | |
| 127 | 41 | Conway | |
| 91 | 91 | 4. | |
| 141 | 78 | Heber Springs | |
| 92 | 73 | Yellville |
Suppose we find ourselves stuck in the middle of Houston and we want to get to Amarillo. (These problems don't have to be realistic, do they?) We have in our hands the following simplified road map of Texas, and we decide to use the A* algorithm. List the cities in the order they are placed into visited. (Note that not all cities will necessarily be visited in the course of the algorithm.)

Houston
Dallas
Fort Worth
Austin
Amarillo [optional]