While trees are a useful data structure for implementing the Set ADT, practitioners tend to use the hash table instead. A tree maintain its elements in order, which is useful in some cases. Hash tables do not maintain any order; this flexibility, as we shall see, results in an opportunity for improved speed.
Before investigating the technique of hashing, though, we'll first examine the important Map ADT, another ADT for which both trees and hashing are useful.
The Map ADT is designed for cases where a program wants to remember associations between objects — that is, where the program wants to maintain a mapping from some collection of objects to another set of objects.
Before we look at the general Map ADT,
we first consider a simple structure called a
An example involving a lookup table would be a program to compute the mode of a set of test scores — that is, the score that occurs most often within a list. There are several ways of computing the mode without using a lookup table. The simplest technique is to go through each element, and for each element count how many other times that element occurs in the list. We return the element with the maximum count. This technique, with two nested loops, each iterating through all elements of the list, takes O(n²) time for n test scores.
We can improve this dramatically, still without using a lookup table, by sorting the list: After sorting, all repeated scores will be adjacent to one another, and we have only to go through the sorted list to find the longest sequence. Sorting the list takes O(n log n) time, and finding the longest sequence takes O(n) time; thus the total time for this algorithm is O(n log n).
Figure 6.1: Finding the mode of an array using a lookup table.
public static int findMode(int[] scores) {
// compute # occurrences of each score
int[] count = new int[101];
for(int i = 0; i < count.length; i++) count[i] = 0;
for(int i = 0; i < scores.length; i++) count[scores[i]]++;
// now find maximum # occurrences
int max = 0;
for(int i = 1; i < count.length; i++) {
if(count[i] > count[max]) max = i;
}
return max;
}
But we can do better using a lookup table. Since the test scores will fall within a restricted range, we can create an array that will track the number of occurrences of each test score. After determining the proper values for this array, we can easily find which element has the largest value. Figure 6.1 illustrates this technique. The first and last loops of Figure 6.1 both take O(1) time relative to n: Both have at most 101 iterations, each iteration taking O(1) time, for a total of O(101 ⋅ 1) = O(1) time. The middle loop, though, has n iterations, so it takes O(n) time.
But suppose we want to be able to find the mode from a list of
strings? Or of points? Or of cities? We might hope to use the
lookup table again, but we couldn't because a lookup table relies
on the elements of the list being used as indices into an array,
and only ints can be used as array indices. What we want
is a different kind of array — one in which any type of data can
be used as an index. This, in fact, is precisely the purpose of the
Map ADT that we'll now examine.
The two abstract data types we have seen thus far,
the List ADT and the Set ADT, operate on
collections of elements — an ordered collection for the List ADT,
an unordered collection for the Set ADT.
The
The Map ADT contains the following operations.
get(k) to retrieve the value associated with the key
k.
put(k, x) to associate the value x
with the key k.
remove(k) to remove any value associated with the key
k.
containsKey(k) to query whether k has a
value associated with it.
keySet to get the set of keys with associated
values.
size to get the number of keys with associated
values.
As you would expect, java.util contains a Map interface
corresponding to the Map ADT. In contrast to the generic classes
and interfaces we have seen so far, which have all had one
generic parameter (like the <E> of List<E>),
the Map interface has two generic parameters, K and
V.
public interface Map<K,V> {
public V get(K key);
public V put(K key, V value);
public V remove(K key);
public boolean containsKey(K key);
public Set<K> keySet();
public int size();
}
In addition to the Map interface, the java.util package also includes a TreeMap class implementing it. The TreeMap works similarly to a TreeSet, but each tree node in a TreeMap contains both a key and a value. The nodes are kept in the tree based on their keys' order.
We can see how to use the Map interface, and the TreeMap
implementation of that interface, by going back to our example
of finding a mode. Suppose we want to find the most commonly
occurring string within an array of names. According to the
logic of the algorithm earlier, we would want a mapping from
strings to integers. And so we'd use a
Map<String,Integer>, as illustrated in
Figure 6.2.
This isn't a straightforward line-by-line translation, but
but it does follow the same basic algorithm.
Figure 6.2: Finding the mode of an array using a hash table.
public static String findMode(String[] names) {
// compute # occurrences of each score
Map<String,Integer> count = new TreeMap<String,Integer>();
for(int i = 0; i < names.length; i++) {
if(count.containsKey(names[i])) {
int oldCount = count.get(names[i]).intValue();
count.put(names[i], new Integer(oldCount + 1));
} else { // first occurrence found
count.put(names[i], new Integer(1));
}
}
// now find maximum # occurrences
String mode = null;
int modeCount = 0;
for(Iterator<String> it = count.keySet().iterator(); it.hasNext(); ) {
String name = it.next();
int nameCount = count.get(name).intValue();
if(nameCount > modeCount) {
mode = name;
modeCount = nameCount;
}
}
return mode;
}
For the TreeMap class, the get and put
operations each take O(log n) time. Thus, each iteration of
the first loop takes O(log n) time; there are n iterations,
for a total of O(n log n) time for the first loop.
Likewise, the second loop takes O(log n) time per iteration,
and there are at most n iterations, for O(n log n) time.
Thus, overall, this approach takes O(n log n) time.
While a TreeMap implements the get and put methods in
O(log n) time, the equivalent operations for a lookup table take
only O(1) time. Unfortunately, the lookup table is applicable only
when the keys happen to be small integers. The idea of hashing
is to figure out a way to leverage the lookup table's performance for
other types of keys. This leads to the HashMap class, an alternative
implementation of the Map interface. In fact, because HashMaps
are faster (and, because they don't involve the Comparable
interface, easier to use), programmers use HashMap much more
often than TreeMap in practice. The
only advantage of TreeMaps is that they keep their keys in order,
but this is not usually very important.
Hashing relies on assuming a
Suppose that we want a map between U.S. states' postal abbreviations
(Strings) and the states' capitals (also Strings). Suppose, also, that
we have an ideal
hash function that maps each state abbreviation
to the position of the state when states are listed in alphabetic
order by their full name; thus, Alabama (
) maps to 0,
Alaska (AL
) maps to 1, etc.AK
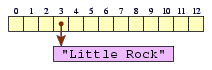
We might tell a HashMap variable map to map Arkansas to
Little Rock.
The HashMap would first query the hash function for the code
for
which would be 3 in this case. Then it would deposit the
associated value into an array.AR,
map.put("AR", "Little Rock");
You can see that the HashMap is simply a lookup table with an added step of applying the hash function to any key to determine the index within the lookup table.
If later we decide to map Alaska to Juneau, we can do that.
map.put("AK", "Juneau");
Now, given a requested to retrieve Arkansas's state capital
(
), we would query the hash function for
Arkansas's hash code (still 3), go to that entry of the table, and
return the string found there (map.get("AR")
).Little Rock
We can continue putting states' capitals into the table, but
what do we do when we get to states whose hash
codes fall outside the array's bounds? For example, what about Kansas
(
), whose hash code is 15, even though the array has
only 13 entries? We'll map such a code into the desired range by
taking the remainder when the code is divided by the array length;
the remainder will be at least
zero but less than the array length, and so it will be a valid
array index. For the Kansas key, we'd divide 15 by 13,
getting a remainder of 2, and so we'd place Topeka at index 2
in the table.KS
map.put("KS", "Topeka");
There are still other problems to address, though.
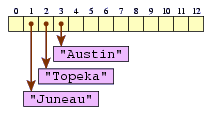
Suppose we decide to map Texas (
) to Austin.
Texas has an index of 42, whose remainder is 3 when divided by 13.
So we'd place Austin at index 3.TX
map.put("TX", "Austin");
Note that this replaced Little Rock.
Now, if we ask our map for Arkansas' capital
(
), we'll get Austin.map.get("AR")
What we have here, with different keys mapping to the same hash
table entry, is called a
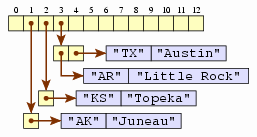
In fact, collisions are quite common. Suppose we decided to hash people based on their birthday. There are 366 different possible hash values, and this hash function is a good one in that it distributes people relatively evenly across them. Even so, an analysis of probabilities says that there will likely be a collision by the time we reach 23 different people.
This phenomenon, in fact, is called the
Now, if we're asked to retrieve the capital associated with Texas, we'll go to the bucket at index 3, and step through the list until we find an entry with Texas as the key. Once found, then we'll return the value in that entry — Austin.
In order to be able to implement a hash table, we must have some way to access the hash function. A hash function must return the same value whenever two instances are equal. Different classes have different definitions of equality between instances. (Think of the different notions of equality between String objects and between Integer objects.) Thus, there is no way to write a generic hash function that covers all possible types of keys.
Java's approach to this is to define two methods — equals and
hashCode — in the Object class, which all classes
ultimately extend.
public boolean equals(Object other) { ...
public int hashCode() { ...
The default implementations (as the methods
are defined in Object) treat two objects as equal exactly when
they are the same object — i.e., they are at the same location
of memory. This matches the notion of equality used with the
== operator: The equals method defined
in the Object class returns true whenever
this == other. A class might override Object's
equals method to define a different notion of
equality; the String class is an example, because two Strings
should be regarded as equal whenever they represent the same
sequence of letters, even if they lie at different locations in
memory. But if it overrides equals, it should also
override hashCode so that two objects that
equals say are equal will also get equal hash codes.
(The String class overrides both.)
The HashMap class will include a private instance variable
table, which will be an array of HashEntries, each being the head
of a list of all entries in the bucket.
(The name table
comes from the term key, we want to access the bucket (to be named
bucket)
corresponding to that key's hash code. This is easy enough.
bucket = table[key.hashCode() % table.length];
This uses the remainder operator (%) to get the
remainder when the hash code is divided by the array's length.
This does not exactly work, though, because the hash code may
be negative, and Java specifies that the remainder operator,
when applied to a negative number, computes a negative
remainder (e.g., (-8) % 3 yields −2).
We can avoid this possibility by adding table.length
to the remainder should it turn out to be negative.
int index = key.hashCode() % table.length;
if(index < 0) index += table.length;
bucket = table[index];
Within each bucket, we want to store objects that associate keys and values together. For this purpose, we'll use the simple HashEntry class.
class HashEntry<K,V> {
private K key;
private V value;
private HashEntry<K,V> next;
public HashEntry(K k, V v, HashEntry<K,V> n) {
key = k; value = v; next = n;
}
public K getKey() { return key; }
public V getValue() { return value; }
public void setValue(V v) { value = v; }
public HashEntry<K,V> getNext() { return next; }
public void setNext(HashEntry<K,V> v) { next = v; }
}
Note that the class has no setKey method. This is
intentional: Once we insert an entry into a bucket, we should
never change the key associated with it, because a different key
would likely belong in another bucket instead.
With the HashEntry class defined, we can now talk about the
proper type for a bucket: Each bucket is a HashEntry, which may itself
be the head of a list of HashEntries.
Thus, the instance variable table is an array of
HashEntries.
private HashEntry<K,V>[] table;
We'll use this within our HashMap implementation found in Figure 6.3, which illustrates how the implementation built into java.util works.
Figure 6.3: The HashMap class.
public class HashMap<K,V> implements Map<K,V> {
private HashEntry<K,V>[] table;
private int curSize;
public HashMap() {
table = (HashEntry<K,V>[]) new HashEntry[13];
curSize = 0;
}
private int getIndex(K key) {
int ret = key.hashCode() % table.length;
if(ret < 0) ret += table.length;
return ret;
}
public int size() { return curSize; }
public V get(K key) {
for(HashEntry<K,V> n = table[getIndex(key)]; n != null; n = n.getNext()) {
if(n.getKey().equals(key)) return n.getValue();
}
return null;
}
public boolean containsKey(K key) {
for(HashEntry<K,V> n = table[getIndex(key)]; n != null; n = n.getNext()) {
if(n.getKey().equals(key)) return true;
}
return false;
}
public V put(K key, V value) {
int index = getIndex(key);
for(HashEntry<K,V> n = table[index]; n != null; n = n.getNext()) {
if(entry.getKey().equals(key)) {
V old = entry.getValue();
entry.setValue(value);
return old;
}
}
table[index] = new HashEntry<K,V>(key, value, table[index]);
curSize++;
return null;
}
public V remove(K key) {
int index = getIndex(key);
HashEntry<K,V> prev = null;
for(HashEntry<K,V> n = table[index]; n != null; n = n.getNext()) {
if(n.getKey().equals(key)) {
if(prev == null) table[index] = n.getNext();
else prev.setNext(n.getNext());
curSize--;
return n.getValue();
}
prev = n;
}
return null;
}
// keySet and iterator methods omitted
}
Hast fast is a HashMap? Its performance depends heavily on how big the
buckets are. If the hash function is reasonably good, then all
buckets will have roughly the same size. Assuming
this, each bucket used in our Figure 6.3
implementation will have roughly n / 13 entries, since that
implementation uses only 13 buckets.
The get and put methods both rely on iterating
through the relevant bucket's entries; since they have close to
n/13 = O(n) entries,
this means that the methods take O(n) time.
Such performance is unacceptable.
The HashMap that is actually implemented in the java.util
package will grow its table we add more entries to it,
just as an ArrayList grows as it receives more values.
In particular, when the number of entries reaches 75% of the number
of buckets, the next call to put will create a new array
for table approximately twice as long as before,
and it will hash all the previous entries into their newly appropriate
buckets.
As with ArrayLists, this will happen infrequently enough
that the O(n) time taken by this doubling procedure
adds only O(1) time to put on average.
The modified put method is in Figure 6.4.
Figure 6.4: When the table is 75% full,
putdoubles the table length.public V put(K key, V value) {
int index = getIndex(key);
for(HashEntry<K,V> n = table[index]; n != null; n = n.getNext()) {
if(entry.getKey().equals(key)) {
V old = entry.getValue();
entry.setValue(value);
return old;
}
}
if(curSize >= table.length * 3 / 4) { // double table length
HashEntry<K,V>[] oldTable = table;
table = (HashEntry<K,V>[]) new HashEntry[table.length * 2];
index = getIndex(key);
for(int i = 0; i < oldTable.length; i++) {
HashEntry<K,V> n = oldTable[i];
while(n != null) {
HashEntry<K,V> next = n.getNext();
int ni = getIndex(n.getKey());
n.setNext(table[ni]);
table[ni] = n;
n = next;
}
}
}
table[index] = new HashEntry<K,V>(key, value, table[index]);
curSize++;
return null;
}
(The 75% amount is called the
With this doubling operation in place to ensure that the average
bucket has O(1) length, both get and
put (and, for that matter, remove and
containsKey) take O(1) time, assuming that
the hash function being used distributes keys approximately
equally across the buckets. The assumption of equal distribution
is important, here: In the worst case, a poor hash function might
end up assigning all keys to the same bucket.
In this case, even though the average bucket may have O(1)
length, the only bucket ever used will have O(n) entries,
and so the methods take O(n) time.
In a moment, we'll investigate how to define good hash functions to
avoid such performance.
Given a good hash function, though, HashMap provides O(1)
performance for get and put, which is an
improvement over TreeMap's O(log n) performance.
So why would anybody ever use TreeMap instead?
HashMaps do have one disadvantage: They don't maintain any
order among the elements in the key set.
Moreover, with the doubling operation, the order may change over
time.
Thus, TreeMap is suitable for
cases where the keys should be maintained in a particular order,
or where for some reason the order of the keys, though not
important, should at least remain consistent.
In practice, such cases are relatively rare,
and thus HashMap is usually the better choice.
The java.util library also defines a HashSet class implementing
the Set interface, which provides O(1) performance for Set's
add, remove, and contains operations,
assuming a good hash function.
This, too, is a marked improvement over TreeSet;
but again, HashSet has the disadvantage that it doesn't maintain
the values in any consistent order.
In cases where the order is unimportant (and these happen more
often than cases where order matters), HashSet is a better
choice than TreeSet.
Until now, we have assumed that a good hash function was already implemented for us. The classes built into Java's libraries, indeed, already have good hash functions defined.
But when we define our own classes that we might possibly use as keys to hash tables, then we need to worry about whether our hash function is suitable. The hash function needs to satisfy two requirements.
The hash code assigned to an object should be consistent over
time. For example, we can't simply return a newly generated random
number each time hashCode is called. If we had such a
hash function, then keys would become lost
in the hash
table.
One consequence of this is that the hash function should not depend on any data within the object that could possibly change in the future.
The hash codes should be consistent with the behavior of
the equals method. That is, if two objects are equal
according to equals, then their hash codes should also
be equal.
This rule has an important consequence: If at any time you want
to override Object's equals method, then you should
also override its hashCode method if there is
a reasonable chance that you or somebody else will want to use
objects of the class as keys in a hash table.
In addition to these two required properties, there is also one property that is highly desirable but not really achievable.
If two objects aren't equal according to equals,
then their hash codes should
not be equal.
There are many situations where this property is impossible to
satisfy: Consider the String class as an example.
There are many more strings than there are valid ints,
and so we could not possibly map every possible distinct string
into a different int.
Since the property is impossible to satisfy, the most we can hope
for is that two unequal objects are likely
to have unequal
hash codes. (Fortunately, String's hashCode method has
this property.)
As an example where you would want to override Object's
hashCode method, consider a class to represent points
with two integer coordinates.
public class Point {
private int x;
private int y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
public int getX() { return x; }
public int getY() { return y; }
public boolean equals(Object other) {
if(!(other instanceof Point)) return false;
Point o = (Point) other;
return o.x == this.x && o.y == this.y;
}
}
In this case, we overrode equals because we want two
points to be regarded as equal any time that their coordinates
match. And whenever we override equals, we should
override hashCode also.
So how can we define hashCode so that any two equal
points receive the same hash code? One simple technique is to
define the hash code be the point's x-coordinate.
public int hashCode() {
return x;
}
This, however, means that any two points with the same
x-coordinate get the same hash code, even if they have
different y-coordinates. But it seems reasonably likely that
in real-world scenarios we might end up with a HashSet or HashMap
involving a cluster of Points, of which several would share the
same x-coordinate. Thus, while this is a valid hash function,
it is not a good one. In general, a hash function ought to take
into account all the data that the equals method takes
into account; here, the equals method relies in part of
the points' y-coordinates, so we should probably include
y in our computation for hashCode, too.
We can write such a hash function by simply adding the x- and y-coordinates.
public int hashCode() {
return x + y;
}
This, though better, still has a shortcoming: Again, consider the possibility of a cluster of points. All points lying on a reverse diagonal (i.e., a line of slope −1) will share the same hash code. For example, points (4, 5) and (3, 6) receive the same hash code, even though they are still rather close.
We can improve the function by multiplying the x-coordinate by some coefficient.
public int hashCode() {
return x * 31 + y;
}
Now, two points will receive the same hash code only if they lie on the same line with slope −31. With integer coordinates, such points would be relatively far apart: For example, the closest points to (4, 5) with the same hash code are (3, 36) and (5, −27). It seems unlikely that somebody would happen to have a set including many such points, so this is a reasonably good hash function. (Technically, due to issues with arithmetic going beyond the range of valid integers, there are other situations where two points receive the same hash code. Having two such points in the same set, though, is unlikely, and so we don't need to worry about it.)
This technique of computing hash codes — taking each relevant
data member, multiplying them by very different coefficients, and
adding the results together — is a common one, because it is
both simple and it provides good results in practice.
In fact, the hashCode method defined by Java's
designers for String is another good example
of this technique. One string is equal to another only if all of the
characters of its string match the other; hence, its hash
function ought really to incorporate information about all the
characters of the string. Java's designers chose the function
where k is the string's length, and si is the character at position i of the string.
With a bit of practice, defining a reasonably good hash function is easy, and that's all that's necessary for being able to use a hash table any time you want a Set or a Map. Hash tables constitute one of the most useful data structures in real computer programming: They are easy to use, efficient in their performance, and flexible in the types of objects they manipulate.
Data & Procedure is licensed under a Creative Commons Attribution-Share Alike 3.0 License.
Based on a work at http://www.cburch.com/books/data/.