Chapter 7. Stacks and queues
We'll now turn our attention to two simple ADTs, the Stack ADT and the Queue ADT. Unlike the other ADTs we have studied (List, Set, Map), these are not represented in the java.util package. Moreover, they do not have any new capabilities beyond those of the other ADTs. In fact, both are special cases of the List ADT. Still, they are important restrictions of the List ADT, and they occur often enough that computer scientists give them special names.
(Actually, the java.util package does include a Stack class and a Queue interface. The Stack class, though, is largely a relic from Java 1.0 and is not a true stack. Likewise, the Queue interface is not a true queue, being intended for more general purposes.)
7.1. Stacks
The Stack ADT is for representing a stack of information, where you can add or remove elements at the top of the stack, but you cannot access data below the top. It includes four operations.
push(x)to addxto the top of the stack.pop()to remove the top element from the stack, returning it.peek()to query what the top element of the stack is.isEmpty()to query whether the stack is currently empty.
The words push and pop are technical terms that computer scientists use to refer to adding and removing elements from a stack.
A stack is sometimes called a last in, first out,
which reflects that with each removal (pop), the value that is
first removed is the value within the stack that was pushed
last.
Stacks are used in many common programs in ways visible to
users, though the programs rarely explicitly use the word
stack.
Web browsers, for example, use a stack to track
pages that have been visited: When you
select a link, the page is loaded and pushed onto a
stack; when you click the Back
button, the top page is
popped off the stack and the page now on the stack's top is displayed.
(Typically, this is not a pure stack, because the browser
usually allows the user to peek at pages beyond the stack's
top.)
Another stack comes in the multiple-undo feature available in
many programs: Each user action is pushed onto a stack,
and selecting Undo
pops the top action off the stack and
reverses it.
7.1.1. Implementing Stack
The Stack ADT is a restriction of the List ADT: The elements are
kept in a particular order, but you can add,
remove, and get only at one end of the list.
For this reason, it's natural to consider using the existing
List data structures, the ArrayList and the LinkedList.
The ArrayList is a good choice: If we maintain the top of the stack at the list's end, then all of ArrayList's relevant operations take O(1) time. This is the inspiration behind the ArrayStack implementation below.
public class ArrayStack<E> {
private ArrayList<E> data;
public ArrayStack() { data = new ArrayList<E>(); }
public void push(E value) { data.add(value); }
public E pop() { return data.remove(data.size() - 1); }
public E peek() { return data.get(data.size() - 1); }
public boolean isEmpty() { return data.size() == 0; }
}
In fact, the java.util package includes a class named
Stack that uses basically this approach. Note that in contrast to
the other ADTs we've studied, the java.util package does not
include a corresponding interface — instead, it includes a class
with that name.
7.1.2. Case study: Program stack
Stacks show up in many situations in the design of computing systems. One of the most important is in remembering the variables of the methods currently in execution.
Each method has a collection of variables that it uses while it
is working, including both the parameter
values and other local variables declared within the method.
This collection of variables is called that method's
Suppose the computer is currently in the process of executing a method A (and so A's activation record is on the top of the stack), and it reaches a point where A's code makes a call to a method B. The computer goes through a three-step process.
It stores its location within A inside A's activation record.
It pushes an activation record for B onto the top of the stack, initializing the variables corresponding to B's parameters based on the values designated by A.
It begins executing the code for B.
As the computer executes B's code, it will have no cause to
access variables of other methods: It will only access B's activation
record, which is on the stack's top.
Eventually, the computer will complete B (likely once it reaches a
return statement within B). Then, the computer
completes two steps.
It pops B's activation record from the top of the stack, so that A's activation record is at the top once again.
It continues executing A, from the location it had previously stored within A's activation record.
All of this occurs as a part of the implementation underlying the execution of Java programs, so it's not something that we can demonstrate in Java code. But understanding how the computer actually processes the execution of methods is a key component to understanding how Java programs work.
7.1.3. Case study: Postfix expression evaluation
Expression evaluation is a case where one might want to use a
stack in Java programs. We'll look at the simplest case of
evaluating expressions given in postfix order. Recall that with
postfix order, the operator is given after the arguments. For
example, the expression normally written 2 + 3
would be written 2 3 +
instead.
The following is a more sophisticated example,
with the corresponding expression tree.
| 4 23 12 − 2 * + |
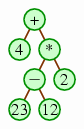
|
A simple approach to evaluating the expression is to use a stack, initially empty, and then go through the expression's elements in order. When we see a number, we'll push that number onto the stack. When we see an operator, we'll pop the top two numbers off the stack and push the result of applying the operator to those two numbers. If the expression is valid, then once we reach the expression's end, the stack will have just one number in it, which will be the overall result of the expression.
In our example, the process would proceed as follows.
| step element stack |
1.4 |
2.23 |
3.12 |
4.- |
5.2 |
6.* |
7.+ |
Since we end up with 26 in the stack, we would conclude that 26 is the correct answer.
This algorithm is easy enough to implement in Java.
Figure 7.1 contains a method whose parameter
is an array of strings, representing the words
within the postfix
expression. It returns the expression's integer value.
Figure 7.1: Evaluating a postfix expression using a stack.
public static int evaluatePostfix(String[] expr) {
Stack<Integer> nums = new Stack<Integer>();
for(int i = 0; i < expr.length; i++) {
String elt = expr[i];
if(elt.equals("+")) {
int b = nums.pop().intValue();
int a = nums.pop().intValue();
nums.push(new Integer(a + b));
} else if(elt.equals("-")) {
int b = nums.pop().intValue();
int a = nums.pop().intValue();
nums.push(new Integer(a - b));
} else if(elt.equals("*")) {
int b = nums.pop().intValue();
int a = nums.pop().intValue();
nums.push(new Integer(a * b));
} else if(elt.equals("/")) {
int b = nums.pop().intValue();
int a = nums.pop().intValue();
nums.push(new Integer(a / b));
} else { // it must be a number
int x = Integer.parseInt(elt);
nums.push(new Integer(x));
}
}
return nums.pop().intValue();
}
Stacks are also useful for evaluating prefix-order expressions and infix-order expressions, but the algorithms are more complex. Calculators that allow parentheses and recognize an order of operations use stacks to evaluate their solution. (In fact, many calculators can be configured so that users can enter expressions in postfix order, because many people who frequently use calculators find postfix order easier to manage. Of course, the calculators use a stack internally.)
7.1.4. Case study: In-order tree traversal
Another place where a stack is useful is in completing an
in-order traversal of a binary tree using an iterator.
Earlier (in Section 5.1.4) we saw how to complete
an in-order traversal using recursion; however,
this recursive technique is not the best technique when we want to write
an iterator — as we need for
TreeSet's iterator method.
For such an iterator, we need some way of remembering
where we currently are in the traversal process, so that each
call to next can step forward to the next element.
We'll use a stack to remember the path of the current tree. In
particular, we'll use a stack named unexplored. The
unexplored stack will hold nodes that we have yet
to iterate through, and whose right subtrees we have yet to
iterate through. At all times, the nodes in the stack will
have the lower nodes within the tree closer to the stack's top;
the stack's top will always be the node holding the next value
in the tree to return.
We'll begin with unexplored holding the path from the
root down to the leftmost node of the tree; note that the
leftmost node will be at the stack's top, which is the first
node we want to return. Thereafter, with each call to
next, we'll pop the top node, push all the nodes
along the path to the leftmost node of the popped node's right
subtree, and then return the popped node's value. The following
sequence illustrates how this works.
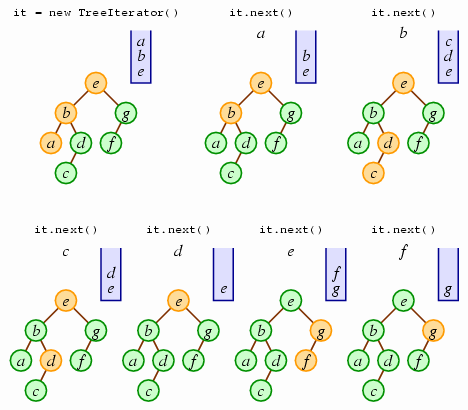
Once the stack becomes empty (as it will be here following one
more call to next), we will have completed the
iteration process.
The TreeIterator class of Figure 7.2 implements this algorithm.
Figure 7.2: The TreeIterator class.
class TreeIterator<E> implements Iterator<E> {
private Stack<TreeNode<E>> unexplored;
public TreeIterator(TreeNode<E> root) {
unexplored = new Stack<TreeNode<E>>();
TreeNode<E> n = root;
while(n != null) { // push left spine of tree onto stack
unexplored.push(n);
n = n.getLeft();
}
}
public boolean hasNext() {
return !unexplored.isEmpty();
}
public E next() {
TreeNode<E> ret = unexplored.pop();
TreeNode<E> n = ret.getRight();
while(n != null) {
unexplored.push(n);
n = n.getLeft();
}
return ret.getValue();
}
}
7.2. Queues
While a stack is a LIFO structure (last in, first out
),
the first in, first out
).
It is similar to a checkout line at a store, where new people
enter at the rear of the line, and they exit only once they
reach the line's front.
The Queue ADT includes four operations.
add(x)to addxto the rear of the queue.remove()to remove the front element from the queue, returning it.peek()to query what the front element of the queue is.isEmpty()to query whether the queue is currently empty.
The Queue ADT can be written as an interface as follows.
In fact, the java.util package includes just such
an interface.
public interface Queue<E> {
public void add(E value);
public E remove();
public E peek();
public boolean isEmpty();
}
Queues are often used in computing systems. For example, networks often have a printer server for each printer, which typically uses a queue to track printing jobs. When the server receives a new printing request, it adds it to the queue; and when the server learns that the printer has completed its current job, it removes from the queue the oldest unprinted job and sends that job on to the printer. This usage of a queue is just like the checkout line in the real world.
Another example comes from network communications: Network routers receive a number of messages to be forwarded on to other destinations. One part of the router is responsible solely for receiving all incoming messages: So that messages aren't lost, it doesn't bother with processing messages yet; this part simply places the message into a queue in memory. Another part of the router works on removing messages from the queue and sending them on to the appropriate next destination.
A final example of a queue is in implementing multiprocessing, the capability of operating systems to appear to run several programs simultaneously. Here, a queue called the ready queue is used to track which programs are ready for execution. When the user requests that the operating system run a program, the program enters the back of the queue. The operating system always has the computer working on a program, and when the system decides that the current program has run long enough, it sends the program to the back of the queue and removes the next program from the queue to run. Because the operating system rotates through programs every few milliseconds, to our eyes it appears that the programs are running simultaneously.
7.2.1. Implementing Queue
An ArrayList is a poor choice for implementing the Queue ADT: Both
additions and removals from the left end (index 0) of an ArrayList take
O(n) time, so whether we locate the queue's front at the
array's left end or the array's right end,
either the add operation (left end) or the
remove operation (right end) will take O(n) time.
We can easily use a linked list, which can manage additions and removals on both ends without any problems.
public class LinkedQueue<E> implements Queue<E> {
private LinkedList<E> data;
public LinkedQueue() { data = new LinkedList<E>(); }
public void add(E value) { data.addLast(value); }
public E remove() { return data.removeFirst(); }
public E peek() { return data.getFirst(); }
public boolean isEmpty() { return data.size() == 0; }
}
This provides O(1) performance for both adding and removing items from the queue.
It would still be nice to use an array, though, because it would
not be as memory-intensive as a linked list.
And, in fact, there is a way that we can use an array, assuming
that we have foreknowledge of the maximum number of elements that
will ever be in the queue. We'll use a wrap-around
technique, where
once we add an element into the final position of the array,
we then wrap around and add the next element into the
initial position. Figure 7.3 contains an
implementation of this concept.
Figure 7.3: Queue implementation based on a wrap-around array
public class ArrayQueue<E> implements Queue<E> {
private E[] data;
private int front; // the index of the front element
private int rear; // the index *after* the rear element
public ArrayQueue(int capacity) {
data = (E[]) new Object[capacity + 1];
front = 0;
rear = 0;
}
public void add(E value) {
data[rear] = value;
rear++;
if(rear == data.length) rear = 0; // wrap around
}
public E remove() {
E ret = data[front];
front++;
if(front == data.length) front = 0; // wrap around
return ret;
}
public E peek() {
return data[front];
}
public boolean isEmpty() {
return front == rear;
}
}
Figure 7.4 illustrates how the queue works through an example. In that example, even though the queue can only hold up to five elements, we manage to add and remove six elements by taking advantage of the wraparound effect.
Figure 7.4: Example illustrating a wraparound queue.
queue after adding 1, 2, 3, 4 remove()returns 1remove()returns 2add(5)add(6)remove()returns 3remove()returns 4remove()returns 5remove()returns 6
This implementation has the shortcoming that we must be very confident of the maximum size the queue will ever be. If the queue ever grows beyond that capacity, it will begin to behave oddly, forgetting about elements in the queue that ought not be forgotten. This shortcoming can be addressed using a doubling technique similar to that used with an ArrayList, although this is somewhat complicated.
7.2.2. Case study: Level-order tree traversal
One example of a situation where a queue is useful is in
performing a
| example tree | level-order traversal |
|---|---|
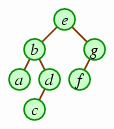
| e b g a d f c |
We can accomplish this through using a queue holding nodes that are roots of subtrees that have yet to be displayed. Initially, the queue will hold the root of the overall tree. With each iteration, we will remove a node yet to be explored, display it, and then add its children so that they will be explored at a later time.
public static void printLevelOrder(TreeNode root) {
Queue<TreeNode> unexplored = new LinkedQueue<TreeNode>();
unexplored.enqueue(root);
while(!unexplored.isEmpty()) {
TreeNode n = unexplored.dequeue();
System.out.println(n.getValue());
if(n.getLeft() != null) unexplored.enqueue(n.getLeft());
if(n.getRight() != null) unexplored.enqueue(n.getRight());
}
}
When we run this on the above example tree, the algorithm will proceed as follows.
| displayed | queue (← front) |
|---|---|
| e | |
| b | |
| g | |
| a | |
| d | |
| f | |
| c |
