Actually, there are a
couple of more sophisticated techniques for implementing the
Priority Queue ADT. The Fibonacci heap supports
add in O(1) time and remove in
O(log n) time. And there is the pair heap, which experiments
indicate is faster than all other techniques, although
researchers are still looking for a proof that its add
method takes O(1) time. Both techniques are more complicated
than we can investigate here, though.
Chapter 8. Priority queues
The
add(x)to addxinto the priority queue.isEmpty()to query whether the priority queue is empty.remove()to remove the highest-priority element from the priority queue, returning it.peek()to query what the highest-priority element of the priority queue is.
Priority queues turn up in several applications. A simple application comes from processing jobs, where we process each job based on how urgent it is. For example, busy dry cleaners may ask each customer when the job must be done, and then they may choose to clean articles of clothing in the order of how little time is left for each article. For that matter, some college students complete assignments based on which is due first. In a similar way, operating systems often use a priority queue for the ready queue of processes to run on the CPU. (The last chapter mentioned that a queue could be used for this purpose, but in fact sophisticated operating systems place priorities on the processes.) Important programs, like those that the user is interacting with, receive a high priority; lower priority is accorded to less urgent tasks like checking periodically for new e-mail or rearranging files on disk for more efficient access. As a result, the operating system works on the background tasks only when the user is not interacting with the computer. We will see some other applications of priority queues later in this chapter.
8.1. Simple priority queue implementations
In using priority queues, one of the problems we confront
is how a program can specify the priorities of the queue's elements.
The java.util package does this with the Comparable
interface: Each element has a compareTo method for comparing to
another element. This compareTo method should return a negative
number if the element should come before the parameter in the priority
queue.
One of the simplest techniques for implementing the
PriorityQueue interface is to use an unordered list, as
illustrated in the ListPQueue class of Figure 8.1.
The add method can simply add the element onto the end of
the list, and the remove method would go through all
elements to determine the minimum, removing and returning that
from the list.
Whether we use an ArrayList or a LinkedList, the
add method would take O(1) time and
remove would take O(n) time.
Figure 8.1: Implementing a priority queue using an unordered list.
public class ListPQueue<E> {
private ArrayList<E> elts;
public ListPQueue() { elts = new ArrayList<E>(); }
public boolean isEmpty() { return elts.size() == 0; }
public void add(E value) { elts.add(value); }
public E peek() {
E min = elts.get(0); // minimum seen so far
for(int i = 1; i < elts.size(); i++) {
Comparable<E> val = (Comparable<E>) elts.get(i);
if(val.compareTo(min) < 0) min = (E) val;
}
return min;
}
public E remove() {
E min = elts.get(0); // minimum seen so far
int minPos = 0; // position of min within elts
for(int i = 1; i < elts.size(); i++) {
Comparable<E> val = (Comparable<E>) elts.get(i);
if(val.compareTo(min) < 0) { min = (E) val; minPos = i; }
}
elts.remove(minPos);
return min;
}
}
Another technique provides the opposite
tradeoff: Rather than store the list with no order,
we can instead store it in descending order.
Now the add method would be complex, involving
locating the proper index for the inserted value and inserting
it at that location. But the remove method would be
quite fast: We simply remove the final element.
Whether we use an ArrayList or a LinkedList, this sorted-list
technique would take O(n) time for add and O(1)
time for remove.
A very different technique uses the binary search tree instead.
For example, we might use the TreeSet class that we saw in
Chapter 5, which already stores its elements in
order according to their compareTo method.
The TreePQueue class defined in Figure 8.2 is
such an example.
Figure 8.2: Implementing a priority queue using a TreeSet.
public class TreePQueue<E> {
private TreeSet<E> elts;
public TreePQueue() { elts = new TreeSet<E>(); }
public boolean isEmpty() { return elts.size() == 0; }
public E peek() { return elts.iterator().next(); }
public void add(E value) { elts.add(value); }
public E remove() {
Iterator<E> it = elts.iterator();
E ret = it.next();
it.remove();
return ret;
}
}
Since the Iterator returned by TreeSet's iterator method
goes through elements in increasing order according to the
elements' compareTo method, and the least among the
elements has the highest priority, the
highest-priority element is the first element returned by the
iterator. Because TreeSet ensures that the tree is always roughly
balanced, this technique supports the add and remove
operations in O(log n) time.
(The TreePQueue implementation of Figure 8.2
contains a bug: With a priority queue, add should always add a
new element, but TreeSet's add method adds a new element
only if an equal element is not already present. We will not
concern ourselves with this distinction, but it is an important
bug.)
8.2. Heaps
A
The heap must be a complete tree. The concept of a complete tree is easiest to explain by example; the following is the only possible structure of a complete tree for 10 nodes.
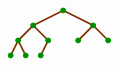
In a complete tree, all nodes in the levels above the bottom two must have two children; and the next-to-last level must have all its non-leaves bunched to the left, all with children excepting the last non-leaf, which may be missing a right child.
Note that a complete tree has a maximum height of 1 + log2 n.
The values of the tree must be in heap order; that is, every node of the heap must have a higher priority than either of its children. The following example illustrates this.
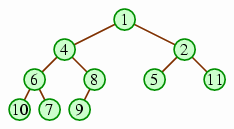
Notice how every number is less than both of its children. As a result, the least number (i.e., the one with the highest priority) will always be at the root of the tree. This heap order is ambiguous: The following, for example, is also a legitimate heap with the same data.
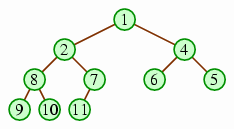
Note the contrast to binary search trees: Binary search trees have a flexible structure; but once the structure is chosen, there is no choice of how to place the values within that structure. In contrast, with heaps, the structure is fixed but the placement of values within the structure is flexible.
When we add a value to a heap, the heap would have to gain a node at the right side of the bottom level. So our addition will initially place the new value in that location; but it may not belong there, because the new value may have a higher priority than its parent. This is easy to address, though: We'll swap the new element and its parent. We can continue the process of swapping up the tree until the new value has a parent with a higher priority, or until the new value reaches the root.
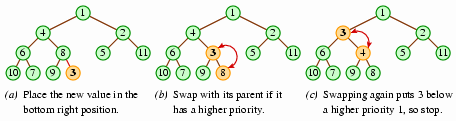
This process maintains the two heap properties, although the formal mathematical argument to this effect is somewhat difficult to make. Note that the addition algorithm takes O(log n) time, since the maximum possible number of swaps is the number of levels, 1 + log2 n.
The process for efficiently removing the highest-priority node (at the
root) is not immediately obvious. You may be tempted to reverse
the addition process: We shift all the values along the path
from the root to the bottom right node up one level; after the
above addition, for example, we would shift the nodes 3, 4, and
8 up, so that 3 would be at the root. This
maintains the first heap property of completeness, but not the second.
(In this case, the root's right child, 2, would have a higher priority
than its parent.)
To preserve the second property, you may be tempted to
trickle
values upward in place of the root; in the above example,
we would place 2 into the root position, and then we'd place 5
into 2's former position. This approach, though, does not
maintain the completeness restriction.
There is a simple O(log n) removal algorithm, though: We'll move the bottom right node to the root, and then we'll trickle it downward, swapping it each step with whichever child has a higher priority, until the higher-priority child is still of lesser priority than the trickling value, or until the value reaches a leaf.
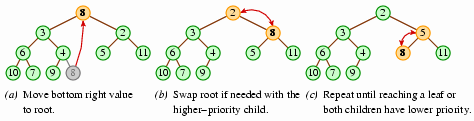
In implementing a heap, we could use the TreeNode class as we did with binary search trees, but there turns out to be a much more convenient representation: We can use an array, storing the values of the tree according to the level-order traversal. Below is a heap drawn in both its tree and its array representations.

In such an array, the root value is in position 0, and a node at position i has its children at positions 2 i + 1 and 2 i + 2. Instead of thinking of a heap as a tree with the above two properties, we can instead think of the heap as an array in which the item at position i has a higher priority than those items at positions 2 i + 1 and 2 i + 2, if they exist. Using an array in this way significantly simplifies programming, and it leads to slightly improved efficiency.
The PriorityQueue class defined in Figure 8.3 uses this representation and implements the above-described addition and removal techniques.
Figure 8.3: Implementing a priority queue using a heap.
public class PriorityQueue<E> {
private E[] data;
private int size;
public PriorityQueue(int capacity) {
data = (E[]) new Object[capacity];
size = 0;
}
public boolean isEmpty() {
return size == 0;
}
public E peek() {
return data[0];
}
public void add(E value) {
int pos = size; // virtual position of value
int pPos = (pos - 1) / 2; // position of parent
size++;
Comparable<E> compValue = (Comparable<E>) value;
while(pos > 0 && compValue.compareTo(data[pPos]) < 0) {
data[pos] = data[pPos]; // move parent into position
pos = pPos; // and step upward
pPos = (pos - 1) / 2;
}
data[pos] = value; // place value in final position
}
public E remove() {
E ret = data[0];
size--; // move last item to root,
Comparable<E> toTrickle = (Comparable<E>) data[size]; // trickle it down
data[size] = null;
int pos = 0;
while(true) {
int less = 2 * pos + 1; // determine lesser of children
if(less >= size) break;
Comparable<E> left = (Comparable<E>) data[less];
if(less + 1 < size && left.compareTo(data[less + 1]) > 0) {
less++;
}
if(toTrickle.compareTo(data[less]) < 0) break;
data[pos] = data[less];
pos = less;
}
data[pos] = (E) toTrickle;
return ret;
}
}
Note that the heap's maximum size must be defined in creating a PriorityQueue object, by passing the maximum size as a parameter into the constructor. A fancier version of the PriorityQueue class would double the array size when a value is added to an already-full heap, as the ArrayList class does; such a PriorityQueue could also include a constructor taking no arguments, implicitly choosing a default initial array size.
We have seen four techniques for implementing priority queues, and we can summarize their performance in a table.
structure addremoveUnordered list O(1) O(n) Sorted list O(n) O(1) Binary search tree O(log n) O(log n) Heap O(log n) O(log n)
In most cases, the heap is the preferred data structure for the Priority Queue ADT.

8.3. Application: Sorting
One of the many applications of priority queues turns up in
sorting. Here, we add all
the elements of an array into a priority queue via the
add method, and then we remove all elements via the
remove method to copy them back into the array.
public static void pQueueSort(Comparable[] data) {
PriorityQueue elts = new PriorityQueue(data.length);
for(int i = 0; i < data.length; i++) elts.add(data[i]);
for(int i = 0; i < data.length; i++) data[i] = elts.removeMin();
}
Both the selection sort and the insertion sort algorithms that we have already seen can be understood as implementations of this technique: For selection sort, our priority queue uses the unordered list representation. Initially, the queue holds all elements, but with each selection of the segment's minimum, the array segment representing the priority queue becomes one element shorter. For insertion sort, our priority queue uses the sorted list representation. The array segment holding the priority queue is initially just the first element alone, but then we add successive elements into the priority queue. Once we've completed removing the elements, the insertion sort algorithm returns them in the order they exist within the priority queue.
We can similarly use a heap to sort numbers, where we designate a portion of the array as the heap, from which we successively remove elements into the undesignated portion, to arrive at a completely sorted array. To do this, we will invert the traditional heap so that each node has a value that is larger than the values of its children, and each removal extracts the heap's maximum value. Our heap will be the first portion of the array; the first phase will be to add all the elements to the heap.
| Heap segment starts with first element only. | ||
| Then we grow it to the first two elements. | 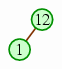 | |
| Then the first three elements. |  | |
| Then the first four elements. | 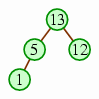 | |
| … until the segment covers the entire array. | 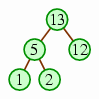 |
In the second phase, we successively remove the maximum value and place it into the appropriate place of the array.
| Remove the heap's maximum into the final slot. |  | |
| The next removal goes into the slot before that. | 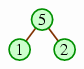 | |
| And the next goes into the slot before that. | 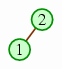 | |
| … until the heap has only one element left. |
This is the idea underlying the from the bottom up,
starting with n / 2
one-node heaps and then merging them.
| We start with the last n / 2 elements being one-node heaps. | ||
| Then we take the next position (where there is a 5), let the two heaps below it be subtrees, and trickle the value downward until we have a heap in that position. | 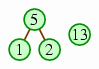 | |
| We repeat the process until there is one heap left. | 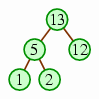 |
We call this process heapSort implementation of Figure 8.4.
Figure 8.4: The
heapSortmethod.public static void heapSort(int[] data) {
// heapify
int size = data.length; // length of heap segment of array
for(int i = (size - 2) / 2; i >= 0; i--) {
trickleDown(data, size, i, data[i]);
}
// remove successive items out of heap
while(size > 1) {
size--;
int toTrickle = data[size];
data[size] = data[0];
trickleDown(data, size, 0, toTrickle);
}
}
private static void trickleDown(int[] data, int size, int pos, int toTrickle) {
while(true) {
int less = 2 * pos + 1;
if(less >= size) break;
if(less + 1 < size && data[less + 1] > data[less]) less++;
if(toTrickle > data[less]) break;
data[pos] = data[less];
pos = less;
}
data[pos] = toTrickle;
}
The advantage of the heapify process is that it is somewhat faster. Creating a heap by adding n elements successively into a single heap takes O(n log n) time, since adding an element into a heap of k elements takes O(log k) time.
However, we can get a better bound with heapifying, because the first n / 2 elements take zero time, the next n / 4 elements can go down only one level, the next n / 8 elements can go down at most two levels, and so on.
It turns out that this sequence can be bounded by n, and so the heapify process takes O(n) time. Using this process, the first phase of Heapsort takes O(n) time. The second phase still takes O(n log n) time, so it does not change the overall speed bound, but the algorithm is marginally faster.

The fact that the sequence can be bounded by n is illustrated by the following table.
| (n/4) | + | (n/8) | + | (n/16) | + … + | 1 | ≤ | n/2 |
| (n/8) | + | (n/16) | + … + | 1 | ≤ | n/4 | ||
| (n/16) | + … + | 1 | ≤ | n/8 | ||||
| : | : | : | ||||||
| 1 | ≤ | 1 | ||||||
| 1 ⋅ (n/4) | + | 2 ⋅ (n/8) | + | 3 ⋅ (n/16) | + … + | (log2 n) ⋅ 1 | ≤ | n |
For each row of the table but the final row, the left side of the inequality contains a geometric sequence, which is approximated on the right. The final row represents the sum of all the rows above: Each column of the final inequality's left side represents the sum of the column entries above. Note that this final inequality's left side matches the expression for the speed of the heapify process. Because it matches the sum of the inequalities above the bottom row, it can be approximated by the sum of the approximations for each of these inequalities, and the sum of these approximations (the table's rightmost column) is itself a geometric sequence that can be approximated by n.
In practice, though they both take O(n log n) time, Heapsort is not quite as fast as Quicksort, because it moves elements around fairly often. Nonetheless, it is an interesting alternative that is quite efficient.
8.4. Application: Shortest path
For another interesting application of priority queues, we consider the problem of finding the shortest distance between two cities on a network of roads. Suppose, for example, that we have the map in Figure 8.5 of roads in the Arkansas Ozarks, and we want to determine the length of the best route from Conway to Mountain Home.
Figure 8.5: An example map of roads in the Arkansas Ozarks.
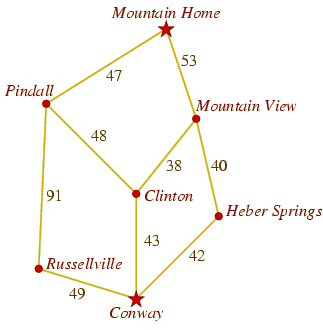
(Mathematicians and
computer scientists call such a network of points
and links a
8.4.1. Dijkstra's algorithm
One of the best possible techniques for computing this distance is
known as
The following pseudocode illustrates this algorithm.
Let known be empty.
Let fringe contain the element (Conway, 0) only.
while Mountain Home ∉ known, do:
Remove city c with smallest distance d from fringe.
if c ∉ known, then:
Add (c, d) to known.
for each neighbor b of c, do:
if b ∉ known, then:
Let x be distance from c to b.
Add (b, d + x) to fringe.
The table of Figure 8.6 illustrates how this would work with the map of Figure 8.5. In it, you can see why our algorithm does not always immediately place cities into known, instead saving them in fringe: In processing Heber Springs, we place Mountain View into fringe. But we discover a shorter route to Mountain View in the next step, when we visit Clinton.
Figure 8.6: A trace of Dijkstra's algorithm on the map of Figure 8.5.
removed (c, d) known fringe initial ∅ (Conway, 0) (Conway, 0) (Conway, 0) (Clinton, 43), (Heber Springs, 42), (Russellville, 49) (Heber Springs, 42) (Conway, 0), (Heber Springs, 42) (Clinton, 43), (Mountain View, 82), (Russellville, 49) (Clinton, 43) (Clinton, 43), (Conway, 0), (Heber Springs, 42) (Mountain View, 81), (Mountain View, 82), (Pindall, 91), (Russellville, 49) (Russellville, 49) (Clinton, 43), (Conway, 0), (Heber Springs, 42), (Russellville, 49) (Mountain View, 81), (Mountain View, 82), (Pindall, 91), (Pindall, 140) (Mountain View, 81) (Clinton, 43), (Conway, 0), (Heber Springs, 42), (Mountain View, 81), (Russellville, 49) (Mountain Home, 134), (Mountain View, 82), (Pindall, 91), (Pindall, 140) (Mountain View, 82) no change (Mountain Home, 134), (Pindall, 91), (Pindall, 140) (Pindall, 91) (Clinton, 43), (Conway, 0), (Heber Springs, 42), (Mountain View, 81), (Pindall, 91), (Russellville, 49) (Mountain Home, 134), (Mountain Home, 138), (Pindall, 140) (Mountain Home, 134) (Clinton, 43), (Conway, 0), (Heber Springs, 42), (Mountain Home, 134), (Mountain View, 81), (Pindall, 91), (Russellville, 49) (Mountain Home, 138), (Pindall, 140)
To implement Dijkstra's algorithm, we would need to choose the
appropriate data structure for both known and
fringe. The only operations on known are
add and contains, so the appropriate ADT for
it would be the Set ADT; and the HashSet would be suitable data
structure.
For fringe, the operations include add and
remove, and so it represents an instance of the
Priority Queue ADT; and a heap would be a suitable structure for
it.
Using a hash table for known and a heap for fringe, we can ask: How much time will Dijkstra's algorithm take to find the best distance? We can try to measure this in terms of n, the number of cities. First, we need to determine the maximum size of fringe. An element b is added into fringe only when b is not in known and we are looking at a c that is in known — so we add an element into fringe only once per road. The number of roads cannot be larger than n², since there are at the most n roads coming from each of the n towns; thus fringe can never have more than n² elements in it.
The inner loop, then, which steps through all the neighbors of c, involves a test for containment within the hash table known — taking O(1) time — and an addition into the heap fringe — taking O(log (n²)) = O(2 log n) = O(log n) time. Thus, each iteration of the inner loop takes a total of O(log n) time. Each city c may have as many as n neighbors, so the inner loop may have as many as n iterations per c, for a total of O(n log n) time.
We will perform this inner loop at most once per city, since we do it only when c is not in known, and then we would also add c into known to ensure that it will not occur again. Thus, the total amount of time spent on the inner loop over the course of the algorithm is O(n² log n). Aside from our time for the inner loop, each iteration of the outer loop takes O(log n) time, since it involves a O(log n) removal from the fringe heap, a O(1) containment test, and a possible O(1) addition to the known hash table. The outer loop may have as many as n² iterations, once for each element added into fringe, for a total of O(n² log n) time spent on the outer loop, neglecting the time spent on the inner loop. The time spent in inner loop overall is also O(n² log n), so the total time is O(n² log n). In terms of big-O notation, Dijkstra's algorithm is essentially the fastest known algorithm for finding the shortest distance between two points on a map.
(Actually, the method presented here is somewhat worse than the best implementation. Using a Fibonacci heap and a slightly modified version of what was presented here, Dijkstra's algorithm provides a bound of O(m + n log n), where m is the number of roads.)
8.4.2. A* search algorithm
Though Dijkstra's algorithm provides the best theoretic
bound known, we can still hope for some practical improvement.
In particular, Dijkstra's algorithm will search in a circle
inflating outward from the starting point; in maps of the real
world, it makes little sense to waste much time with the side of
the circle that is farther away from the destination. It would
be better if the bubble
would inflate more quickly toward
the destination. This is the idea underlying the
With A* search, we require some … that we can compute quickly
prevents
us from using the true distance. If we could already determine that
quickly, there would be no point in trying to solve the problem.)
For a map, the natural heuristic function would be the crow's
distance
— that is, the length of a straight-line flight
from the city in question to the destination.
Figure 8.7 enhances our earlier map with some
heuristic values.
Figure 8.7: A map with heuristic values.

city h(city) Clinton 52 Conway 86 Heber Springs 63 Mountain Home 0 Mountain View 36 Pindall 34 Russellville 88
Once we have a heuristic function, then we'll associate with each city c in fringe an estimate of the distance from the start location to the destination via c — we'll add the known distance from the start location to c and the heuristic distance from c to the destination. Below is the modified algorithm; the notation h(x) represents the heuristic value for the city x.
Let known be empty.
Let fringe contain the element (Conway, 0, h(Conway)) only.
while Mountain Home ∉ known, do:
Remove element (c, d, e) from fringe where e is smallest.
if c ∉ known, then:
Add (c, d) to known.
for each neighbor b of c, do:
if b ∉ known, then:
Let x be distance from c to b.
Add (b, d + x, d + x + h(b)) to fringe.
Figure 8.8 illustrates how the A* search algorithm would perform on our earlier problem, using the heuristic function listed in Figure 8.7.
Figure 8.8: A trace of the A* search algorithm on the map of Figure 8.7.
removed (c, d, e) known fringe initial ∅ (Conway, 0, 52) (Conway, 0, 52) (Conway, 0) (Clinton, 43, 95), (Heber Springs, 42, 105), (Russellville, 49, 137) (Clinton, 43, 95) (Conway, 0), (Clinton, 43) (Heber Springs, 42, 105), (Russellville, 49, 137), (Mountain View, 81, 117), (Pindall, 91, 125) (Heber Springs, 42, 105) (Conway, 0), (Clinton, 43), (Heber Springs, 42) (Russellville, 49, 137), (Mountain View, 81, 117), (Pindall, 91, 125), (Mountain View, 82, 118) (Mountain View, 81, 117) (Clinton, 43), (Conway, 0), (Heber Springs, 42), (Mountain View, 81) (Russellville, 49, 137), (Pindall, 91, 125), (Mountain View, 82, 118), (Mountain Home, 135, 135) (Mountain View, 82, 118) no change (Russellville, 49, 137), (Pindall, 91, 125), (Mountain Home, 135, 135) (Pindall, 91, 125) (Clinton, 43), (Conway, 0), (Heber Springs, 42), (Mountain View, 81), (Pindall, 125) (Russellville, 49, 137), (Mountain Home, 135, 135), (Mountain Home, 138, 138) (Mountain Home, 135, 135) (Clinton, 43), (Conway, 0), (Heber Springs, 42), (Mountain View, 81), (Pindall, 125), (Mountain Home, 135) (Russellville, 49, 137), (Mountain Home, 138, 138)
You can see that it takes slightly fewer iterations that before; in particular, it concluded early on that there was little point in examining Russellville, even if it was close to Conway, because the heuristic function indicated that it was so far from Mountain Home. If we were doing A* on a more complete map, including cities south of Conway, the difference between the real performance of Dijkstra's algorithm and the A* algorithm would be even more noticable.
Using the same analysis as for Dijkstra's algorithm, the big-O bound on the A* search algorithm's performance is the same O(n² log n). Without allowing room for some quantification of the heuristic function's accuracy (which would be quite complicated), we cannot improve on this bound.
Dijkstra's algorithm and A* search algorithm demonstrate a sophisticated usage of the analysis we have seen in this book, applied to a useful problem. Our analysis involved two data structures — hash tables and heaps — of the several important data structures we have seen. This is just one of the many important, practical, and interesting problems where the analytic tools and the knowledge of data structures that we have investigated have proven useful.
