Chapter 17. Recursion

We saw how to create methods in Chapter 12. Inside their bodies, we can include invocations of other methods. It may not have occurred to you, but you might reasonably wonder: Could a method invoke itself?

Self-invocation may at first sound useless or illegal: Isn't this defining something in terms of itself — what is called a circular definition? But self-invocation is legally, and it's actually quite useful. In fact, it's so useful that it gets its own special name: recursion. We'll explore recursion in this chapter.

17.1. A first example

Let us begin with an example and see how it works.

Figure 17.1: A Mystery program.
1 import acm.program.*; 2 3 public class Mystery extends Program { 4 public void run() { 5 int result = compute(4); 6 println(result); 7 } 8 9 public int compute(int n) { 10 if(n == 1) { 11 return 1; 12 } else { 13 return n * compute(n - 1); // here's the recursive invocation 14 } 15 } 16 }

The program of Figure 17.1 defines compute, which is recursive because it invokes itself on line 13. Let's step through the program and see how it will work.

run(): We start, of course, in the run method. This program immediately invokes compute with a parameter of 4. This will temporarily suspend work on run until the invocation compute(4) completes.
compute(4): With the parameter variable n having the value 4 as assigned, we run through compute. Since 4 isn't 1 (line 10), we go into the else clause. On line 13, we find we must invoke a method named compute with a parameter of 3. Thus, we temporarily suspend our work until this recursive invocation compute(3) completes.
compute(3): We now run through compute with the parameter n being 3. Since 3 isn't 1, we go into the else, where we find we must recursively invoke compute with a parameter of 2. Thus, we temporarily suspend our work until this recursive invocation compute(2) completes.
compute(2): We now run through compute with the parameter n being 2. Since 2 isn't 1, we go into the else, where we find we must recursively invoke compute with a parameter of 1. Thus, we temporarily suspend our work until this recursive invocation compute(1) completes.
compute(1): We now run through compute with the parameter n being 1. Since the if condition is turns out to be true, we go to line 11, which say we should return 1. This completes the invocation to compute(1).
compute(2): We had previously suspended the invocation of compute(2) at line 13 until compute(1) completed. It has now finished, so we pick up where we left off at line 13. This line says to return n * compute(n - 1). We just finished with determining that compute(n - 1) returns a value of 1, so we now want to return n * 1. Since n has a value of 2 in this current invocation of compute, we end up returning the value of 2 * 1, which is 2.
compute(3): We had suspended the invocation of compute(3) at line 13 until compute(2) completed. It has now finished, returning a value of 2. We are to return n * compute(n - 1). Since n has a value of 3 in this invocation of compute, and we just finished with determining that compute(n - 1) has a value of 2, we return 6 (that is, 3 ⋅ 2).
compute(4): We had suspended the invocation of compute(4) at line 13 until compute(3) completed. It has now finished, returning a value of 6. We are to return n * compute(n - 1). Since n has a value of 4 in this invocation of compute, and we just finished with determining that compute(n - 1) has a value of 6, we return 24 (that is, 4 ⋅ 3).
run(): We had suspended the invocation of run() at line 5 until compute(4) completed. It has now finished, returning a value of 24. Thus, we assign the result variable to refer to 24 and we continue to the next line, which will display 24 for the user to see.

What this program manages to do is to display the value of 4 ⋅ (3 ⋅ (2 ⋅ 1)). That is, it displays the product of the numbers from 4 down to 1. More generally, what this compute method does is to return the product of all the integers between 1 and its parameter n. Mathematicians call this product the factorial of n, and indeed the program would be better if its compute method were given the more descriptive name of factorial — but then what it does wouldn't be much of a mystery any more for those who knew the term.

17.2. How recursion works

You'll notice that the compute method doesn't always recur: When its parameter n is 1, the method simply returns immediately without any recursive invocations.

With a bit of thought, you'll realize that any functional recursive method must have such a situation, since otherwise, the recursive method will never finish. In fact, these situations are important enough to merit a special term: Any condition where a recursive method does not invoke itself is called a base case.

But what exactly happens when a recursive method lacks a base case? To understand this, we need to get some idea about how a computer handles method invocations.

In executing a program, the computer creates what is called the program stack. The program stack is a stack of frames, each frame corresponding to a method invocation. At all times, the computer works on executing whichever method is at the stack's top; but when there is a method invocation, the computer creates a new frame and places it atop the stack. When the method at the stack's top returns, the computer removes that method's frame from the stack's top, and resumes its work on the method now on the frame's top. (This removal process is sometimes called popping the stack; the addition process (when a method invocation takes place) is sometimes called pushing.)

To see how this works, let's diagram how the Mystery program operates.

1.		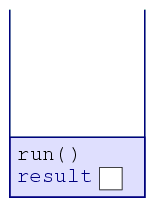To start off the program, the program pushes a frame corresponding to an invocation to `run()`. Notice how this frame includes room for `run`'s variable `result`.
2.		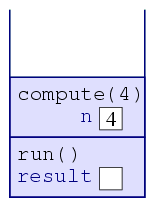When the computer sees that `run()` invokes `compute(4)`, the computer places a new frame atop the stack corresponding to `compute`; this frame will include the variable `n`, whose value is initially 4.
3.		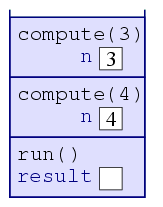When the computer sees that `compute(4)` invokes `compute(3)`, the computer places a new frame atop the stack, containing the variable `n`, whose value is initially 3.
4.		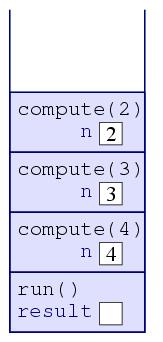When the computer sees that `compute(3)` invokes `compute(2)`, the computer places a new frame atop the stack, containing the variable `n`, whose value is initially 2.
5.		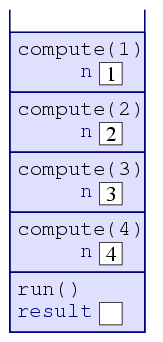When the computer sees that `compute(2)` invokes `compute(1)`, the computer places a new frame atop the stack, containing the variable `n`, whose value is initially 1.
6.		When the computer sees that `compute(1)` returns, it pops the top frame off the stack and resumes with whatever frame is now at the top — which happens to be the frame for `compute(2)`.
7.		When the computer sees that `compute(2)` returns, it pops the top frame off the stack and resumes with `compute(3)`.
8.		When the computer sees that `compute(3)` returns, it pops the top frame off the stack and resumes with `compute(4)`.
9.		When the computer sees that `compute(4)` returns, it pops the top frame off the stack and resumes with `run()`. The `run()` invocation assigns the valued returned to its `result` variable, which modifies the variable in its frame.
10.		As the computer executes the method atop the stack, `run`, it sees that the method invokes `print`. It thus pushes `print(24)` onto the stack. In fact, `print` will push additional methods onto the stack, which are all eventually popped off.
11.		Once `print` returns, the computer pops its frame off the stack and continues executing `run`. In fact, `run` will return promptly (since there is nothing else to do in that method). Thus, its frame will be popped off, too. Once the stack is empty, the computer halts execution of the program.

So what happens if a recursive method never reaches a base case? The stack will never stop growing. The computer, however, limits the stack to a particular height, so that no program eats up too much memory. If a program's stack exceeds this size, the computer initiates an exception, which typically would crash the program. (From the operating system's point of view, crashing the program is preferable to allowing a program to eat up too much memory and interfere with other better-behaved programs that may be running.) The exception is labeled a StackOverflowError.

So any time you see a StackOverflowError, the most likely cause is that there is some sort of recursion going on, and that recursion never reaches a base case. In fact, this would occur with the Mystery program if we simply the 4 in line 5 to a 0.

17.3. Recursion versus iteration

You may object: How is this useful? I could just as easily have written the program using a loop!

public class Factorial extends Program { public void run() { int n = 4; int result = 1; while(n > 0) { result *= n; n--; } println(result); } }

Indeed, you could. And indeed, most professional programmers would prefer that you did. Thus, while you might acknowledge that the Mystery program works, it just doesn't provide any evidence that recursion can be useful. In Chapter 18, we'll see some examples where recursion is indeed the best way to approach a problem. But before looking at those examples, we still have more to do as far as solidifying our understanding of recursion.

But this objection brings up another important point: Recursion and loops are actually related concepts. Generally, anything you can do with a loop, you can do with recursion, and vice versa. Sometimes one way is simpler to write, and sometimes the other is, but in principle they are interchangeable. In fact, some programming languages don't even have any loops (such as Haskell), and other programming languages don't permit recursion (FORTRAN 77). Nonetheless, people manage to write sophisticated programs using them. Most modern languages in wide use, though, take the position that programmers ought to be able to choose which is most appropriate for the problem.

It's useful for us to take some programs using a loop and to see how to rewrite them using recursion. I'd quickly admit that these aren't compelling examples for why recursion is useful, since the programs would be more simply written using a loop. But such examples really are the best with which to start learning about how to write recursive methods.

17.3.1. Reversing a string

We begin with our earlier program that reads a line from the user and displays it in reverse order.

Figure 17.2: The Reverse program.
3 public class Reverse extends Program { 4 public void run() { 5 String str = readLine("Type a string to reverse: "); 6 int index = str.length() - 1; 7 while(index >= 0) { 8 print(str.substring(index, index + 1)); 9 index--; 10 } 11 } 12 }

Our goal is to remove the usage of the while loop and to replace it with a recursive method. To do this, we'll need to introduce a new method, which we'll call printReverse.

public class ReverseRecur extends Program { public void run() { String line = readLine("Type a string to reverse: "); printReverse(line); } public void printReverse(String str) { } }

Now the question is how to write the body of this method. To do this, we'll rely on what I'll call the magical assumption:

Magical Assumption: Assume that our recursive method already magically works for all smaller instances of the parameter.

In our case, we're writing printReverse so that it prints the parameter string str in reverse. The magical assumption will be that printReverse will somehow work for all strings that are shorter than str. In continuing, then, we'll ask: How can we use this assumption to print all of str in reverse?

Of course! I hope you respond (or at least you will with some more practice). What we should do is to first print the last letter of str, then we apply the magical assumption to str with the last letter removed! For example, if we have str referring to the string straw, our method will first display the last letter w, then recursively invoke the method on stra. Since stra has fewer letters than straw, this recursive invocation (says our magical assumption) will displays its reverse arts, thus completing the output of warts.

This approach translates into the following code.

print(str.substring(str.length() - 1)); printReverse(str.substring(0, str.length() - 1));

(Incidentally, you might have responded that we should first apply the magical assumption to str with the first letter removed (traw), then finally to print the first letter (s). That is also a valid response, and I'm not going to get caught up arguing which is better.)

But this approach doesn't entirely work: The program is missing a base case. For this, we wonder: What's the smallest possible parameter? Of course, it would be a string with no letters in it at all. And in that case, we don't want to display anything. We use this to build our final program in Figure 17.3.

Figure 17.3: A recursive version of Reverse.
3 public class ReverseRecur extends Program { 4 public void run() { 5 String line = readLine("Type a string to reverse: "); 6 printReverse(line); 7 } 8 9 public void printReverse(String str) { 10 if(!str.equals("")) { 11 print(str.substring(str.length() - 1)); 12 printReverse(str.substring(0, str.length() - 1)); 13 } 14 } 15 }

Note that the test in line 10 tests to see whether the base case does not apply. I wrote it this way because, in the case that the base case does apply, we don't want to do anything. It would look odd to have an if statement without anything in its braces and then an else clause, so instead I inverted the condition: If the string isn't empty, then we do the recursion.

Of course, we wrote this thinking solely in terms of our magical assumption, which doesn't immediately convince us that the program will work. But it does.

Given the parameter straw, the method displays an w and invokes itself recursively with the parameter stra.
That recursive invocation (with stra as a parameter) displays an a and invokes itself recursively with the parameter str.
That recursive invocation (with str) displays an r and invokes itself recursively with the parameter st.
That recursive invocation (with st) displays a t and invokes itself recursively with the parameter s.
That recursive invocation (with s) displays an s and invokes itself recursively with an empty string as a parameter.
That recursive invocation (with an empty string) does nothing.
As each of the recursive invocations picks up where it left off, they have nothing more to do.

The overall result is that the program has displayed warts as required.

17.3.2. Counting letters

Let's do another example. Suppose I want to count the number of r's in a string typed by the user. (Remember, the useful examples are coming later….) We can do this using iteration easily enough.

Figure 17.4: The CountRs program.
3 public class CountRs extends Program { 4 public void run() { 5 String str = readLine("Type a string to analyze: "); 6 int index = 0; 7 int count = 0; 8 while(index < str.length()) { 9 if(str.substring(index, index + 1).equals("r")) { 10 count++; 11 } 12 index--; 13 } 14 println("There are " + count + " r's."); 15 } 16 }

This time, when we convert it to a recursive method taking a string as a parameter, it will be a method that returns an integer. This is so that the run method will be able to receive an integer that it can then display.

public class CountRs extends Program { public void run() { String line = readLine("Type a string to analyze: "); int count = countRs(line); println("There are " + count + " r's."); } public void countRs(String str) { } }

To write the recursive countRs method, we again apply the magical assumption: We have a parameter named str, but we suppose that any invocation of countRs on a string shorter than str somehow manages to return the numbers of r's in that shorter string. This leads to an implementation where we examine the first letter of the string to see if it is an r, and then use a recursive invocation to count the r's in the remainder of the string.

int k = 0; if(str.substring(0, 1).equals("r")) { k++; } k += countRs(str.substring(1)); return k;

Once again, though, we're missing the base case, which is when the string is empty. In that case, we want to return 0. We conclude with the full, working implementation.

Figure 17.5: A recursive version of CountRs.
3 public class CountRs extends Program { 4 public void run() { 5 String line = readLine("Type a string to analyze: "); 6 int count = countRs(line); 7 println("There are " + count + " r's."); 8 } 9 10 public void countRs(String str) { 11 if(str.equals("")) { 12 return 0; 13 } else { 14 int k = 0; 15 if(str.substring(0, 1).equals("r")) { 16 k++; 17 } 18 k += countRs(str.substring(1)); 19 return k; 20 } 21 } 22 }

17.3.3. Perfect numbers

A positive integer is said to be perfect if the sum of its factors (excluding the integer itself) is that integer. For example, 6 is perfect, since the numbers that divide into it exactly are 1, 2, 3, and 6, and the sum of 1, 2, and 3 is itself 6. So also is 28 perfect: Its factors are 1, 2, 4, 7, 14, and 28, and 1 + 2 + 4 + 7 + 14 = 28.

Suppose we want a program to determine whether a number is perfect. We could do it easily enough using a loop.

Figure 17.6: The Perfect program.
3 public class Perfect extends Program { 4 public void run() { 5 int query = readInt("Type an integer: "); 6 int index = 1; 7 int sum = 0; 8 while(index < query) { 9 if(query % index == 0) { 10 sum += index; 11 } 12 index++; 13 } 14 if(sum == query) { 15 println(query + " is perfect"); 16 } else { 17 println(query + " isn't perfect: The sum is " + sum); 18 } 19 } 20 }

But of course, for the sake of practice, we want to write this using recursion instead. We start by writing our recursive method.

3 public class PerfectRecur extends Program { 4 public void run() { 5 int query = readInt("Type an integer: "); 6 int sum = sumFactors(query); 7 if(sum == query) { 8 println(query + " is perfect"); 9 } else { 10 println(query + " isn't perfect: The sum is " + sum); 11 } 12 } 13 14 public int sumFactors(int num) { 15 } 16 }

But now we hit a brick wall: Try as we might, the magical assumption just doesn't help us. Knowing the sum of the factors up to 1, 2, 3, 4, and 5 just doesn't help with determining the sum of the factors up to 6.

The way over this brick wall is to introduce an additional parameter for our recursive method. This additional parameter will correspond to the index variable in our initial loop-based solution.

3 public class PerfectRecur extends Program { 4 public void run() { 5 int query = readInt("Type an integer: "); 6 int sum = sumFactorsTo(query, query - 1); 7 if(sum == query) { 8 println(query + " is perfect"); 9 } else { 10 println(query + " isn't perfect: The sum is " + sum); 11 } 12 } 13 14 public int sumFactorsTo(int num, int max) { 24 } 25 }

This helps to put us back on track: Given a query of 6, this code will invoke sumFactorsTo with two parameters, 6 and 5, with the intent of summing all the factors of 6 between 1 and 5 — or, more generically, given the two parameters num and max, the method should return the sum of the factors of num between 1 and max. To do this, we'll first determine the sum of all the factors of num between 1 and max − 1; we can do this utilizing the magical assumption, since max − 1 is smaller than max. Then we can add max if it itself is a factor of num and return that.

Again, though, we need to worry about the base case. As we descend into the recursion, each layer has max being 1 smaller than before. Once it reaches 0, we should descend no further: This will be our base case. In this case, there are no numbers between 1 and 0, so we'll return 0.

All the above reasoning is encoded in the program of Figure 17.7.

Figure 17.7: A recursive version of Perfect.
3 public class PerfectRecur extends Program { 4 public void run() { 5 int query = readInt("Type an integer: "); 6 int sum = sumFactorsTo(query, query - 1); 7 if(sum == query) { 8 println(query + " is perfect"); 9 } else { 10 println(query + " isn't perfect: The sum is " + sum); 11 } 12 } 13 14 public int sumFactorsTo(int num, int max) { 15 if(index == 0) { 16 return 0; 17 } else { 18 int sub = sumFactorsTo(num, max - 1); 19 if(num % max == 0) { 20 sub += max; 21 } 22 return sub; 23 } 24 } 25 }