Often programs must manipulate many similar objects. For example, if we were writing a program for searching the library's catalog, we might imagine that the program would have a different object for each book. We could hope to have a separate variable referencing each object, but this isn't practical if our program deals with thousands of objects (as with our library example). Luckily, Java provides a construct called an array for this situation.
An
To create a variable for referencing an array, use a variable declaration of the following form.
<typeOfElement>[] <arrayVariableName>;
For example, the following creates a variable score
that can reference an array of numbers.
double[] score;
This creates a variable that can reference an array. Like object
variables, it does not actually reference an array yet.
To create an array and assign the array variable to reference it, we
will use the new keyword.
score = new double[6];
This is the syntax for creating an array: the new keyword,
followed by the type name of each array element, followed by the length
of the array enclosed in brackets. The integer in brackets can be any
expression (
instead of 2 * numStudents
,
for example).3
Creating such an array sets up the score variable to look as
follows in the computer's memory. (The numbers in the array, however,
all default to 0.)
To work with an array, we reference individual elements according to
their
Yes, that's one less than the array length.
So if you declare an array score of length 3,
the three array indices are 0, 1, and 2, since Java always begins
numbering from 0.
(Starting from 0 turns out to be more convenient than the intuitive
choice of 1.)
So even though the array has a length of 3, there is no array element
with an index of 3
If you try to access an undefined array index,
the program will crash with an
ArrayIndexOutOfBoundsException.
So be careful with array indices.
To refer to an array element in an expression, type the array variable name, followed by the element's array index enclosed in brackets. You can also do this on the left-hand side of an assignment statement to alter an array element's contents.
double[] score = new double[3];
score[0] = 97.0;
score[1] = 83.0;
score[2] = 66.0;
println("Average = " + ((score[0] + score[1] + score[2]) / 3.0));
In these statements we create an array of three numbers,
called score. We assigned its three boxes to refer to three
test scores, 97, 83, and 66. And finally we printed the
average of these. The computer will display 82.0.
The significance of arrays comes when you use an expression to access a particular element of the array. Figure 19.1 contains a short program that reads a sequence of numbers into an array and then prints the numbers in reverse order. For example, the user might experience the following in running the program. (What the user types is in boldface.)
How many scores? 3 Type the scores now. 2 3 5 Here they are in reverse order. 5.0 3.0 2.0
There's no way we could write a program to accomplish this using what we had seen in previous chapters. Using arrays, however, allows us to store an arbitrarily large sequence of data with no troubles.
Figure 19.1: The
PrintReverseprogram.1 import acm.program.*;
2
3 public class PrintReverse extends Program {
4 public void run() {
5 // create the array
6 int num_scores = readInt("How many scores? ");
7 double[] score;
8 score = new double[num_scores];
9
10 // fill the array
11 for(int i = 0; i < num_scores; i++) {
12 score[i] = readDouble("Score " + i + ": ");
13 }
14
15 // print it in reverse
16 println("Here they are in reverse order.");
17 for(int i = num_scores - 1; i >= 0; i--) {
18 println(" " + score[i]);
19 }
20 }
21 }
Java includes a special technique for accessing the length of an
array, using the word length. In any expression, you can
write the array name, followed by a period and the word length,
and the value will be the number of items that the array was created to
hold.
As an example, we could rewrite
line 11 of
Figure 19.1 as follows.
for(int i = 0; i < score.length; i++) { //@ num_scores
It's preferable to use the length keyword when
appropriate, in favor of using some other variable that happens to
represent the length of the array.
You'll recall that the String class provides a length
method that returns the number of characters in a string. Thus, if we
want to know how long the String referenced by a variable
name is, we use
.name.length()
With arrays, though, length is a special word
built into Java, not a method. As a result, parentheses are not
applied to length when used with an array.
To determine how long the array
referenced by score, we type
,
not score.length
.score.length()
We'll now consider a more complex problem. Suppose we have an array of test scores, all integers between 0 and 100, and we want to find the mode — that is, the integer occurring most often. We'll see two techniques for computing this.
In the more obvious technique, found in Figure 19.2, we'll go through each number in the array and count how many times that number appears in the array. As we go along, we track which number has appeared most often. Once we complete counting each number in the array, we'll have found the mode.
Figure 19.2: The
computeModemethod.public int computeMode(int[] nums) {
int maxValue = -1;
int maxCount = 0;
for(int i = 0; i < nums.length; i++) {
// count number of times nums[i] is in array
int count = 0;
for(int j = 0; j < nums.length; j++) {
if(nums[j] == nums[i]) {
count++;
}
}
// remember the highest count we have seen
if(count > maxCount) {
maxValue = nums[i];
maxCount = count;
}
}
return maxValue;
}
An alternative technique is to create a second array, which I'll call
tally, which initially has 0 throughout. We then go through the
array of test scores, and with each score k, we increment
entry k of tally. By the end of this process,
tally[i] will hold the number of times i appears among the
test scores. Our last step is to see which entry in tally is
largest; the index of this entry is the mode.
Figure 19.3: The
tallyModemethod.public int tallyMode(int[] nums) {
// create array of tallies, all initialized to zero
int[] tally = new int[101];
for(int i = 0; i < tally.length; i++) {
tally[i] = 0;
}
// for each array entry, increment corresponding tally box
for(int i = 0; i < nums.length; i++) {
int value = nums[i];
tally[value]++;
}
// now find the index of the largest tally - this is the mode
int maxIndex = 0;
for(int i = 1; i < tally.length; i++) {
if(tally[i] > tally[maxIndex]) {
maxIndex = i;
}
}
return maxIndex;
}
This second technique can often be significantly faster: It looks at each test score only once, whereas the first technique will look at each test score as many times as there are test scores. That is, if our parameter array contains n test scores, the first technique will look into the array n² times, whereas the second technique will look into the array only n times.
So far we have been working with arrays of numbers. But we can have arrays of any type of thing we want. For example, suppose we want to simulate a ball bouncing around a window with several circular bumpers inside it.
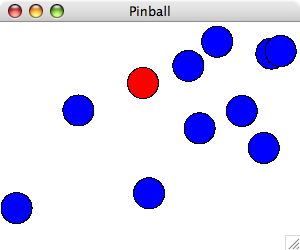
We might want to store the bumpers as an array of
GOvals. Creating such an array is easy enough.
GOval[] bumper = new GOval[10];
However, this doesn't itself create an array of 10 GOval
objects: It creates 10 GOval variables, which can potentially
reference GOval boxes. But these array entries default to
null, and it is our job to populate the array with references
to GOval objects.
for(int i = 0; i < bumper.length; i++) {
double x = Math.random() * (getWidth() - 30);
double y = Math.random() * (getHeight() - 30);
bumper[i] = new GOval(x, y, 30, 30);
bumper[i].setFilled(true);
bumper[i].setFillColor(new Color(0, 0, 255));
this.add(bumper[i]);
}
The following diagram illustrates what will be in memory after the array has been populated.
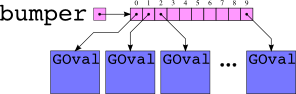
Figure 19.4 contains a complete program implementing a ball bouncing off of circular bumpers. The logic involved uses a tad of trigonometry. This isn't the point of this chapter, so I'll conveniently avoid explaining it here.
Figure 19.4: The
Pinballprogram.import acm.program.*;
import acm.graphics.*;
import java.awt.*;
public class Pinball extends GraphicsProgram {
public void run() {
// Create the ball that will bounce around the screen
GOval ball = new GOval(25, 25, 30, 30);
ball.setFilled(true);
ball.setFillColor(new Color(255, 0, 0));
this.add(ball);
// Create the bumpers off of which the ball will bounce
GOval[] bumper = new GOval[10];
for(int i = 0; i < bumper.length; i++) {
double x = Math.random() * (getWidth() - 30);
double y = Math.random() * (getHeight() - 30);
bumper[i] = new GOval(x, y, 30, 30);
bumper[i].setFilled(true);
bumper[i].setFillColor(new Color(0, 0, 255));
this.add(bumper[i]);
}
double theta = Math.PI / 6; // ball's current direction
while(true) {
// wait for one frame, step ball once in current direction
this.pause(20);
ball.move(3 * Math.cos(theta), 3 * Math.sin(theta));
// update direction if bounce off window's edge or bumper
double x = ball.getX();
double y = ball.getY();
if(x < 0 || x + 30 >= this.getWidth()) {
theta = Math.PI - theta; // hits window's left/right edge
} else if(y < 0 || y + 30 >= this.getHeight()) {
theta = -theta; // hits window's top/bottom edge
} else {
for(int i = 0; i < bumper.length; i++) {
double dx = bumper[i].getX() - x;
double dy = bumper[i].getY() - y;
if(dx * dx + dy * dy < 30 * 30) { // hits bumper
double in = Math.atan2(dy, dx);
theta = (in + Math.PI) - (theta - in);
}
}
}
}
}
}
Programming via Java is licensed under a Creative Commons Attribution-Share Alike 3.0 License.
Based on a work at http://www.cburch.com/books/java/.
